Maturità Scientifica 2017 – Questionario – Quesito 9
Maturità Scientifica 2017 – Questionario – Quesito 9 – Matematica
Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.
[el58862bfc101c9]
Traccia del Quesito 9 del Questionario Maturità Scientifica 2017
Dimostrare che l’equazione arctan(x) + x3 +ex = 0 ha una e una sola soluzione reale.

Maturità Scientifica 2017 – Questionario – Quesito 9
Svolgimento:
Questo nono quesito del questionario della maturità scientifica 2017 è quasi esclusivamente teorico e richiede di dimostrare l’esistenza di un’unica soluzione reale. Per chiarire un po la situazione può essere d’aiuto disegnare il grafico dei tre addenti-funzioni separatamente e sommati.
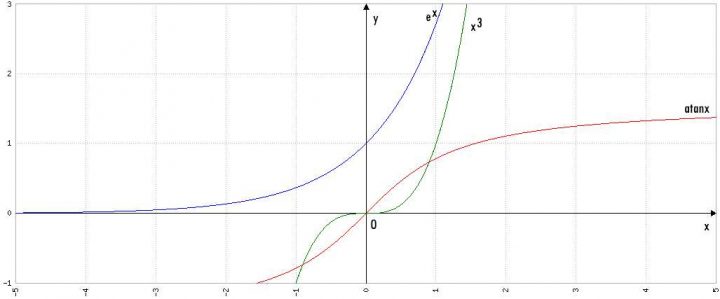
Le tre funzioni – Questionario Quesito 9 Maturità Scientifica 2017
Dai grafici è chiaro che si ha un un unica intersezione della funzione con l’asse delle ascisse, circa a x=-0,5; tuttavia non dobbiamo calcolarne il valore, ma dimostrarne l’esistenza e poi l’unicità. Si cercherà quindi di applicare il Teorema dell’esistenza degli zeri, il quale recita che: data una funzione f(x) continua nell’intervallo chiuso e limitato [a,b], se essa assume valori di segno opposto in corrispondenza di a e in b, ovvero se f(a) ⋅ f(b)<0, allora esiste almeno uno zero di tale funzione.
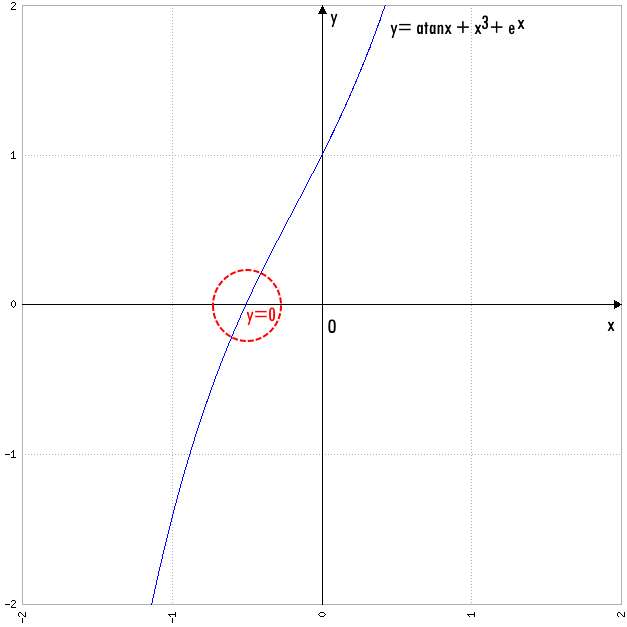
Grafico e zero della funzione – Questionario Quesito 9 Maturità Scientifica 2017
Dal secondo grafico osservo che questo zero ricade nell’intervallo [-1;0] che è comunque contenuto nel dominio della funzione (che è tutto R), per cui limitato. Le funzioni addendo sono continue per definizione e la loro somma sarà ancora una funzione continua. Passo pertanto al calcolo di f(-1) e f(0).
f(x) = arctan(x) + x3 +ex
f(-1)= arctan(-1)+(-1)3+ e-1= – 3.14 -1 + 0,37= -3,77 < 0
f(0)= arctan(0)+(0)3+ e0= 0 + 0 + 1 =1 > 0
f(a)⋅f(b) = (-3,77)⋅(+1)<0 → Esiste almeno uno zero.
Rimane da dimostrare l’unicità di questo zero. Per fare questo occorre utilizzare il Teorema di unicità dello zero, che aggiunge una ulteriore condizione al precedente teorema: Se f(x) è una funzione continua in [a,b], derivabile in (a,b) , f(a)⋅f(b) <0 e f'(x) è diversa da zero in (a,b) , allora esiste un solo valore c in (a,b) in cui la funzione si annulla.
Quindi devo considerare l’intervallo aperto (a,b) e dimostrare che qui la funzione è derivabile e lo è perchè somma di funzioni derivabili; il prodotto dei valori assunti agli estremi è già stata soddisfatta: f(a)⋅f(b) < 0. Controlliamo se la derivata prima non si annulla mai.
f(x) = arctan(x) + x3 +ex
f'(x) = (1+x2)-1 + 3x2 +ex
Si osserva subito che i tre addendi sono sempre strettamente positivi, in particolare nell’intervallo [-1,0] per cui la derivata non è mai nulla. Questo garantisce l’unicità dello della soluzione.
Link per approfondire la prova di maturità scientifica 2017, matematica.
- Vai al Questionario – Quesito 1 – 2017
- Vai al Questionario – Quesito 2 – 2017
- Vai al Questionario – Quesito 3 – 2017
- Vai al Questionario – Quesito 4 – 2017
- Vai al Questionario – Quesito 5 – 2017
- Vai al Questionario – Quesito 6 – 2017
- Vai al Questionario – Quesito 7 – 2017
- Vai al Questionario – Quesito 8 – 2017
- Vai al Questionario – Quesito 9 – 2017
- Vai al Questionario – Quesito 10 – 2017
- Vai al Problema 1 – Quesito 1 – 2017
- Vai al Problema 1 – Quesito 2 – 2017
- Vai al Problema 1 – Quesito 3 – 2017
- Vai al Problema 1 – Quesito 4 – 2017
- Vai al Problema 2 – Quesito 1 – 2017
- Vai al Problema 2 – Quesito 2 – 2017
- Vai al Problema 2 – Quesito 3 – 2017
- Vai al Problema 2 – Quesito 4 – 2017
- Teorema dell’esistenza degli zeri (o di Bolzano) – Wikipedia
- Teorema dell’unicità dello zero e altri richiami di teoria- (Prof. Fernando D’Angelo, PDF)