Maturità Scientifica 2017 – Problema 2 – Quesito 4
Maturità Scientifica 2017 – Problema 2 – Quesito 4 – Matematica
Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.
[el58862bfc101c9]
Traccia del Problema 2 della Maturità Scientifica 2017 – Quesito 4
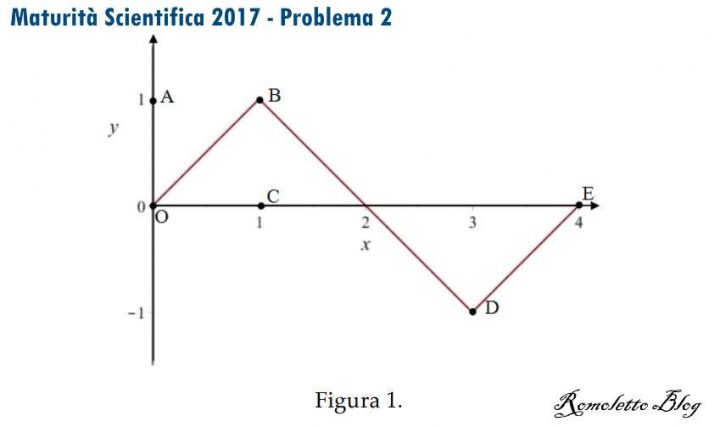
Consideriamo la funzione f : R → R , periodica di periodo T=4 il cui grafico, nell’intervallo [0;4], è il seguente:
Figura 1 Problema 2 Quesito 3 Maturità Scientifica 2017
Come si evince dalla Figura 1, i tratti OB, BD, DE del grafico sono segmenti i cui estremi hanno coordinate:
O(0; 0), B(1; 1), D(3; −1), E(4; 0).
Quesito 4: Determina infine il volume del solido generato dalla rotazione attorno all’asse y della porzione di piano compresa tra il grafico della funzione h per x∈ [0; 3] e l’asse
delle x.
Svolgimento:
La funzione h(x) viene fuori dalla risoluzione del quesito 1:
![]()
Avevamo trovato che:
x∈[0,1); k=0
x x 1
h(x)=∫ t dt = [½t2 ] = ½x2 → [½x2] = ½
0 0 0
x∈[1,3); k=0
x x
h(x)= ½ + ∫ (2-t) dt = [2t – ½t2 ] =
1 1
= ½ +(2x – ½x2 – 2 + ½) =
= 2x – ½x2 – 1
3
[2x – ½x2 – 1] =6-(9/2)-1 = ½
0
x∈[3,4); k=1
x x
h(x)=½ +∫ (t-4) dt = [½t2 – 4t] =
3 3
= ½ + (½x2 – 4x – (9/2)+12 ) =
= [½x2 – 4x + 8]
Possiamo dunque raccogliere i vari risultati e scrivere:
/ ½x2 , x∈[0,1)
h(x)= < 2x – ½x2 – 1 x∈[1,3)
\ ½x2 – 4x + 8 x∈[3,4)
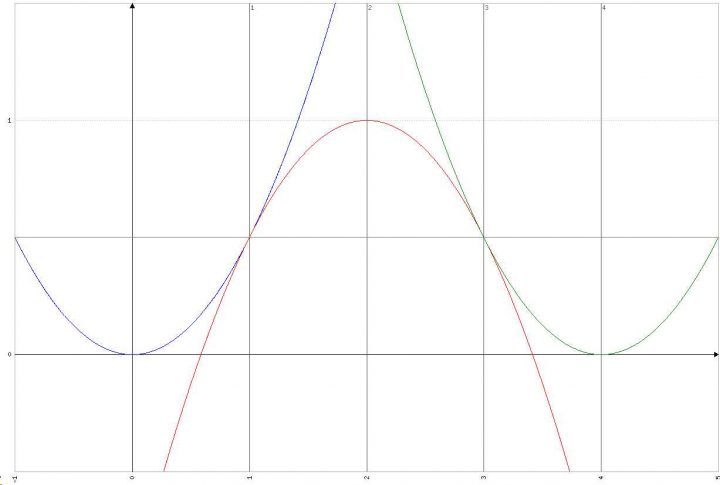
Grafico della funzione h(x) del Problema 2 Quesito 1 Maturità Scientifica 2017
Per il calcolo del volume di un solido di rotazione è sufficiente calcolare l’area di una “fettina” di funzione f(x) e moltiplicarla per 2πx, dove x è la sua distanza dal punto di rotazione. Questo quesito nasconde “una piccola insidia” nel senso che dobbiamo stare attenti al fatto che l’asse di rotazione è l’asse y. In questo caso infatti il volume si calcola, in generale:
x2
Vrot= 2π∫ xf(x)dx
x1
Particolarizzando:
1 1
Vrot_1= 2π∫x(½ x2 )dx =(2π/8)[x4 ]= π/4
0 0
3
Vrot_2= 2π∫x(2x – ½x2 – 1 )dx =
1
3 3 3
= 2π (∫2x2 dx – ∫½x3 dx – ∫x dx) =
1 1 1
3 3 3
= 2π {[(2/3)x3] – [(1/8)x4 ] – [(1/2)x2]}=
1 1 1
= 2π {[(54/3) – (2/3)] – [(81/8)-(1/8) – [9/2 -(1/2)]} =
=2π{(52/3) – (80/8) – (8/2)}=
=2π{52-30-12}/3=
=20π/3
A questo punto sommando:
Vrot=Vrot1=+Vrot2=
=[(1/4)+(20/3)]π =
= π(3+80)/12=
= 83π/12
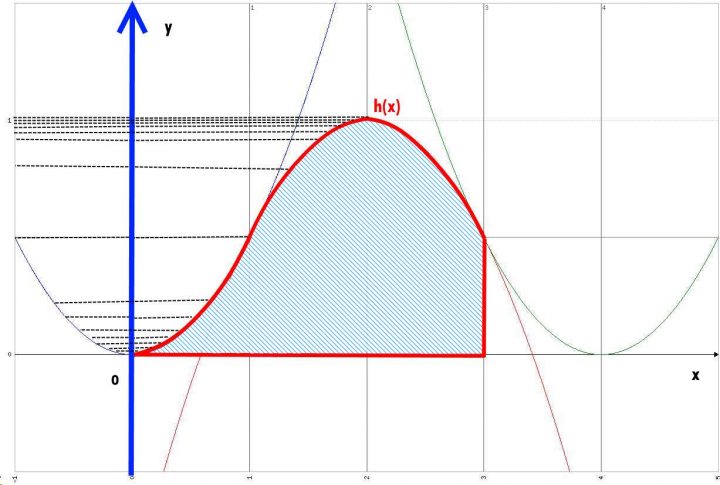
Volume del solido di Rotazione Problema 2 Quesito 4 Maturità Scientifica 2017
Link per approfondire la prova di maturità scientifica 2017, matematica.
- Vai al Questionario – Quesito 1 – 2017
- Vai al Questionario – Quesito 2 – 2017
- Vai al Questionario – Quesito 3 – 2017
- Vai al Questionario – Quesito 4 – 2017
- Vai al Questionario – Quesito 5 – 2017
- Vai al Questionario – Quesito 6 – 2017
- Vai al Questionario – Quesito 7 – 2017
- Vai al Questionario – Quesito 8 – 2017
- Vai al Questionario – Quesito 9 – 2017
- Vai al Questionario – Quesito 10 – 2017
- Vai al Problema 1 – Quesito 1 – 2017
- Vai al Problema 1 – Quesito 2 – 2017
- Vai al Problema 1 – Quesito 3 – 2017
- Vai al Problema 1 – Quesito 4 – 2017
- Vai al Problema 2 – Quesito 1 – 2017
- Vai al Problema 2 – Quesito 2 – 2017
- Vai al Problema 2 – Quesito 3 – 2017
- Vai al Problema 2 – Quesito 4 – 2017
- Integrale solido di rotazione (wikipedia)