Maturità Scientifica 2017 – Problema 1 – Quesito 3

by Romoletto Blog · 29 Giugno 2017

Maturità Scientifica 2017 – Problema 1 – Quesito 3 – Matematica

Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.

[el58862bfc101c9]

Traccia del Problema 1 della Maturità Scientifica 2017 – Quesito 3

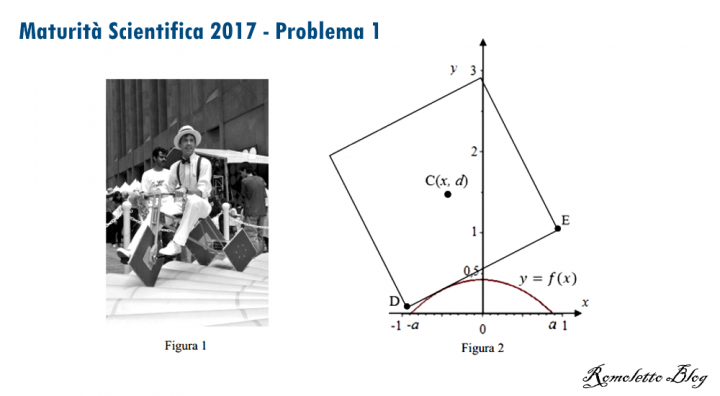
Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New York, al MoMath-Museum of Mathematics si può fare, in uno dei padiglioni dedicati al divertimento matematico (figura 1). È però necessario che il profilo della pedana su cui il lato della ruota può scorrere soddisfi alcuni requisiti. In figura 2 è riportata una rappresentazione della situazione nel piano cartesiano Oxy: il quadrato di lato DE= 2 (in opportune unità di misura) e di centro C rappresenta la ruota della bicicletta, il grafico della funzione f(x) rappresenta il profilo della pedana.

Maturità Scientifica 2017 – Problema 1

Romoletto Blog ti consiglia...
Bull Burner Brucia Grassi Potenti Veloci, Drenante Forte Dimagrante Efficace, 120 Capsule per Dimagrire Velocemente Donna e Uomo con Glucomannano, Carnitina, Bromelina, Te' Verde - Prodotto in Italia
Programma perdita di peso di 30 giorni: programma drenante brucia grassi di 30 giorni: 120 pillole di alta qualità made in italy progettate per sostenere le diete dimagranti.. Formula potente: contiene glucomannano (1200 mg), l-carnitina, bromelina e tè verde efficaci ...
Nota: prodotto fornito da Amazon

Quesito 3: Considerando la similitudine dei triangoli rettangoli ACL e ALM in Figura 4, e ricordando il significato geometrico della derivata, verifica che il valore dell’ordinata d del centro della ruota si mantiene costante durante il moto. Pertanto, al ciclista sembra di muoversi su una superficie piana.

Svolgimento:

Il terzo quesito chiede al solito una verifica, ma nell’impostazione occorre qualche momento di ragionamento in più. Facciamo un ingrandimento e consideriamo i triangoli ALC e ALM.

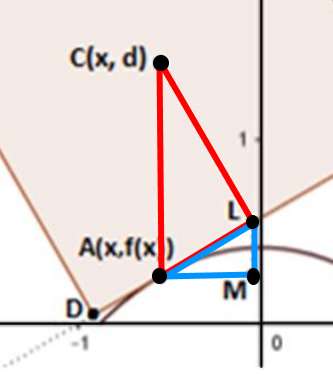
Triangoli simili – Ingrandimento – Maturità scientifica 2017

La distanza d(C,r: y=0)=d è costante. Notiamo che nella posizione iniziale (e finale), ovvero quando C e D (o C ed E) sono allineati verticalmente, la distanza CD corrisponde alla semidiagonale del quadrato e sappiamo che rimarrà costante:

ricordando che il rapporto tra lato è diagonale di un quadrato è d = l· √2
d = (2*√2)/2 = √2

Questa distanza d inoltre è la somma tra AC e f(x) ovvero l’ordinata di A:

d = AC+f(x) = √2

ci manca AC; inoltre sappiamo che:

CL=lato/2 = 1;

se i triangoli sono simili hanno rispettivi lati proporzionali e angoli congruenti:

AC:AL=AL:LM=CL:AM
CAL=ALM; ACL=LAM; ALC=AML

Quindi, poichè ci occorre AC:

AC:AL=CL:AM → AC=AL·CL/AM → AC=AL/AM

Mi serve AL e AM. Il quesito chiede esplicitamente di riprendere il significato geometrico di derivata. La derivata geometricamente rappresenta il valore della tangente in un punto di ascissa x; f'(x) = tan(α) *:

Δy=LM; Δx=AM → (LM/AM)=tan(α)=f'(x) (α=LAM)

che posso riscrivere, per la similitudine tra i triangoli, come:

(AL/CL)=tan(α)=f'(x).

In definitiva, poichè CL=1 si ha che:

(LM/AM)=(AL/CL)=AL=tan(α)=f'(x),

Cosi mi accorgo che per calcolare AC posso ricorrere anche al Teorema di Pitagora, evitando cosi di cercare di calcolare AM:

AC=√ CL²+AL² = (1+f'(x)²)^½

A questo punto calcolando:

f'(x) = (e^-x– e^x)/2 ; (e^-x– e^x)²= e^-2x+e^2x-2

Sostituendo otteniamo:

AC={1+[(e^-x– e^x)/2] ²}^½ =
= {1+ [e^-2x+e^2x-2]/4}^½ =
= ½ {4+e^-2x+e^2x-2}^½ =
= ½ {2+e^-2x+e^2x}^½ =
= ½ {2+(1/e^2x) + e^2x– 2 }^½ =
= ½ {(2e^2x+1 + e^4x)/e^2x}^½ =
= ½ {(2e^2x+ 1 + e^4x)/e^2x}^½ =
= ½ {[(e^2x+ 1)²]/e^2x}^½=
= ½ {[(e^2x+ 1)²]/e^2x}^½=
=½ {(e^2x+ 1)/e^x}=
= ½ (e^x + e^-x)

Poichè sappiamo già che

d = AC+f(x) = √2 ,

allora verifichiamo che sia vero. Sostituendo si ha infatti che:

d = [ ½ (e^x + e^-x)] + [√2 – ½ (e^x + e^-x)]= √2

CVD

Note

* La derivata è in realtà definita come il limite del rapporto incrementale Δy/Δx per Δx che tende a zero. In questo caso considerare valori finiti Δx e Δy o valori infinitesimi dx e dy non fa variare l’angolo α in quanto si ha il vincolo per cui il segmento AL per quanto piccolo possa diventare, per come è costruito, sta sempre sul lato DE del quadrato.