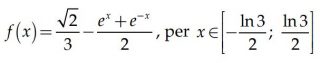Maturità Scientifica 2017 – Problema 1 – Quesito 4

by Romoletto Blog · 30 Giugno 2017

Maturità Scientifica 2017 – Problema 1 – Quesito 4 – Matematica

Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.

[el58862bfc101c9]

Traccia del Problema 1 della Maturità Scientifica 2017 – Quesito 4

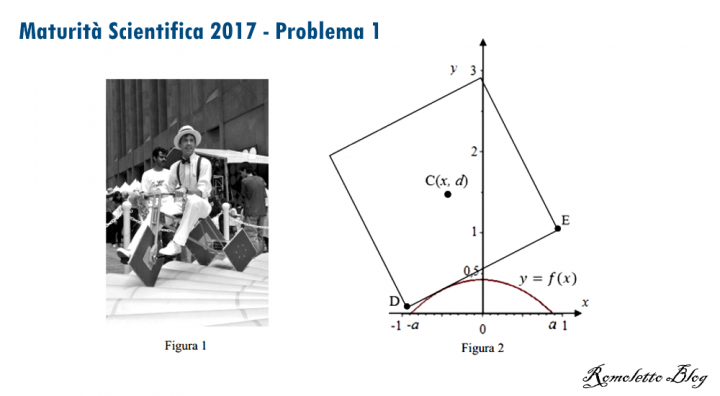
Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New York, al MoMath-Museum of Mathematics si può fare, in uno dei padiglioni dedicati al divertimento matematico (figura 1). È però necessario che il profilo della pedana su cui il lato della ruota può scorrere soddisfi alcuni requisiti. In figura 2 è riportata una rappresentazione della situazione nel piano cartesiano Oxy: il quadrato di lato DE= 2 (in opportune unità di misura) e di centro C rappresenta la ruota della bicicletta, il grafico della funzione f(x) rappresenta il profilo della pedana.

Maturità Scientifica 2017 – Problema 1

Romoletto Blog ti consiglia...
Caffè Borbone Don Carlo, Kit Degustazione - 60 Capsule
Miscele 20pz.Blu/10pz.Rossa/10pz.Dek/10pz.Oro/10pz.Nera. Miscele assortite. Compatibili con macchine a marchio lavazza* a modo mio*. *lavazza , *a modo mio , *lavazza a modo mio , *espresso point e *lavazza espresso point sono marchi di proprietà di luigi lavazza s.P.A. . Caffè ...
Nota: prodotto fornito da Amazon

Quesito 4: Anche il grafico della funzione:

se replicato varie volte, può rappresentare il profilo di una pedana adatta a essere percorsa da una bicicletta con ruote molto particolari, aventi la forma di un poligono regolare. Individua tale poligono regolare, motivando la risposta.

Svolgimento:

Il quarto quesito chiede di effettuare in pratica delle operazioni “inverse” rispetto a quelle fatte nei quesiti precedenti, ovvero si ha l’equazione di vuole risalire al poligono che può percorrere questa catenaria con posizione del centro C costante.

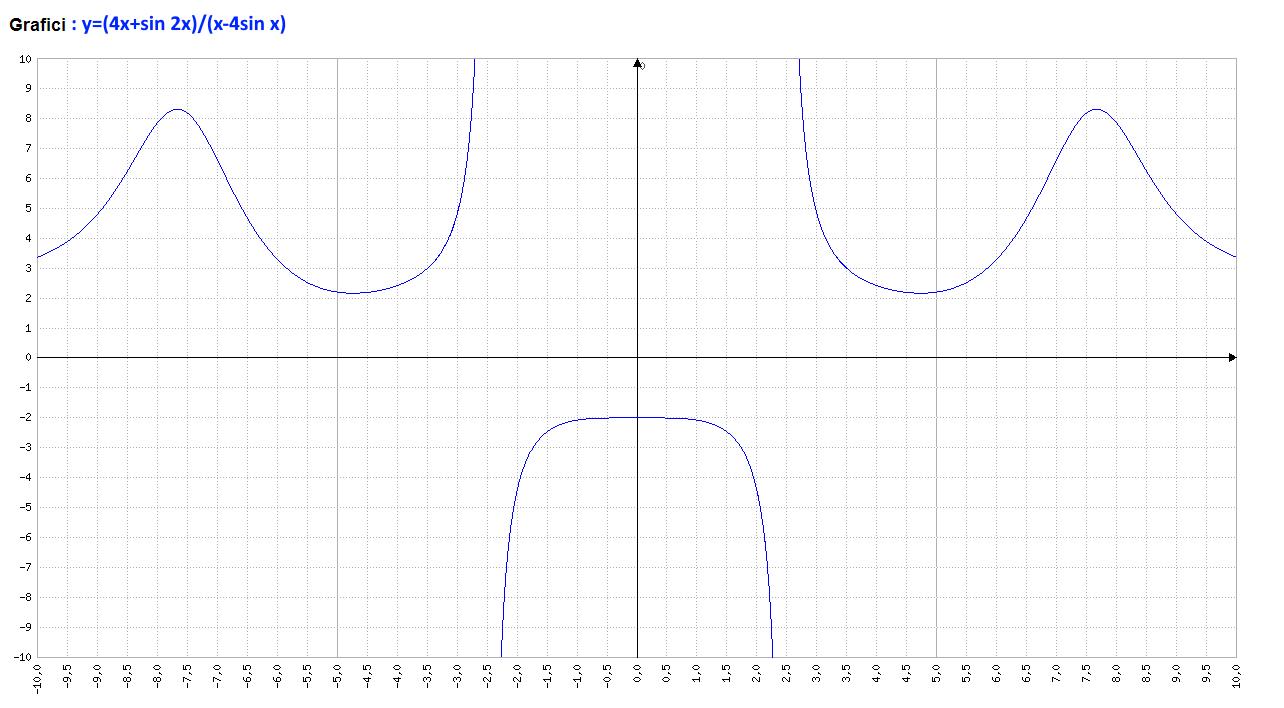
Riconsiderando il quesito 2, avevamo provato che i tratti del grafico iniziali e finali erano tra di loro perpendicolari, proprio in virtù del fatto che i vertici del quadrato (angolo retto) devono incastrarsi perfettamente. Il grafico della funzione è il seguente:

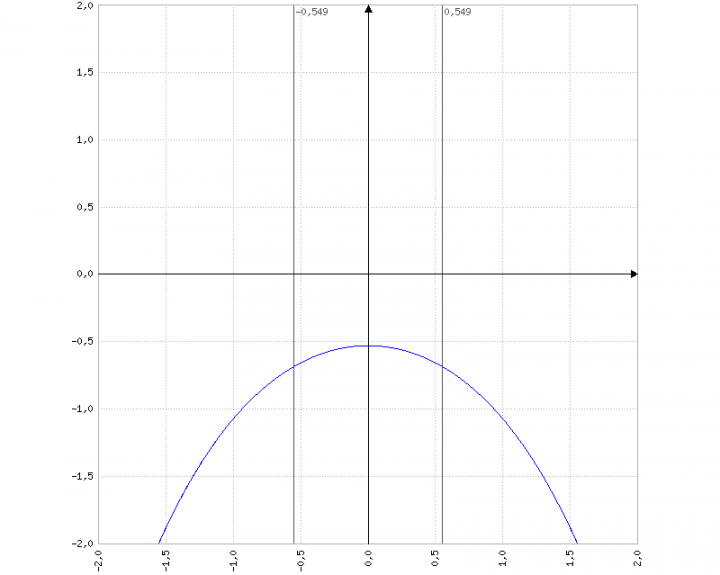
Angoli Poligono Problema 1 Quesito 4 Maturità Scientifica 2017

Grafico Equazione Problema 1 Quesito 4 Maturità Scientifica 2017

Seguendo questo ragionamento, possiamo scoprire l’angolo formato dai tratti in questione e quindi di che poligono si tratta. Dobbiamo cioè calcolare quanto valgono le derivate agli estremi della funzione data. La derivata è identica a quella del quesito 2, solo che deve essere calcolata in (-½ ln(3)) e (+½ ln(3)):

f'(x) = (e^-x– e^x)/2

Sostituendo:

f'(-½ ln(3))⁺=½ (e^{-(-½ ln(3))} – e^{-½ ln(3)}) =
= 3^½-3^-½ = ½(2/√3) = (√3)/3

Per simmetria l’altra dovrebbe essere -(√3)/3, controlliamo:

f'(+½ ln(3))^–=½ (e^{-(½ ln(3))} – e^{½ ln(3)}) =
= 3^-½– 3^½ = ½(-2/√3) = -(√3)/3

Quindi abbiamo ottenuto una tan α =(√3)/3 e una tan β =(-√3)/3. L’angolo corrispondente è α=arctan(√3)/3= 30° e β =arctan (-√3)/3 = 150°.

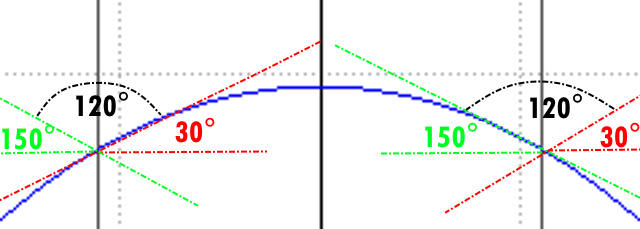
Angoli Poligono Problema 1 Quesito 4 Maturità Scientifica 2017

L’angolo interno del poligono regolare è quindi 150°- 30°=120° e l’unico a poter avere angoli tutti da 120° è l’esagono.

Note

A riprova -pratica- del ragionamento, basta rieseguire o ricontrollare il calcolo effettuato per la f(x) di partenza del quesito 1,

la quale ha fornito tan α = 1 e una tan β = -1 i cui angoli corrispondenti sono α = arctan(1) = 45° e β =arctan (-1) = 135° e la cui differenza è appunto 90° (valore assunto da tutti gli angoli di quadrato).