Maturità Scientifica 2017 – Questionario – Quesito 6 – Matematica

Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.

Traccia del Quesito 6 del Questionario Maturità Scientifica 2017

Determinare il numero reale a in modo che il valore di

sia un numero reale non nullo.

Maturità Scientifica 2017 – Questionario – Quesito 6

Svolgimento:

Questo sesto quesito del questionario della maturità scientifica 2017 richiede lo studio del limite di cui sopra, al variare dell’esponente a. Tra tutti i valori di a si devono trovare quelli che lo rendono non nullo e finito.

Il parametro a può assumere qualsiasi valore in R. Cominciamo pertanto dal caso che sembra più immediato: a=1. Il limite diventa in parte notevole:

l=lim (sinx-x)/x =
    x→0

= lim(sinx/x)-1=
    x→0

= lim 1-1=0
   x→0

Quindi non siamo stati fortunati. Consideriamo allora tutti i valori di a>1.

 l=lim (sinx-x)/x^a =
    x→0

= lim (1/x^(a-1)) (sinx/x)-1=
   x→0

= lim ((sinx/x)-1)/(x^(a-1))=
x→0

Non porta a nulla di buono;

=lim (1-1)/0= 0/0
x→0

E’ una forma indeterminata, applichiamo, al limite di partenza, de l’Hopital:

 l = lim (sinx-x)/x^a  →(H)→
  x→0

D(sinx – x) = cosx-1
D(x^a) = ax^(a-1)

 =lim(cosx-1)/ax^a-1 = 0/0
  x→0

Se però poniamo a=3 il limite diventa notevole:

 lim -(1/3)[(1-cosx)/x² ] = 
 x→0

= -(1/3)*(1/2)= -1/6

che è un valore reale e finito. Potremmo aver concluso, occorre però considerare tutti gli intervalli rimanenti. Essendo, prima di effettuare la sostituzione a=3, il limite ancora una forma 0/0, riapplichiamo de l’Hopital:

 lim (cosx-1)/ax^a-1  →(H)→
  x→0

D a(cosx – 1) = -asinx
D(x^a-1) =(a-1) x^(a-2)

 =lim k[-sinx]/[x^a-2] =0/0 = 
   x→0

(con k indico la parte numerica, per comodità) e riapplichiamo de l’Hopital ancora  →(H)→

 =lim k'(cosx)/x^a-3 = ∞
   x→0

Se quindi a>1 dobbiamo studiare due sottocasi:

se 1<a<3 l’esponente diventa negativo, ciò significa moltiplicare per zero si otterrà quindi un valore del limite pari a zero.

Se a>3 allora il limite vale infinito.

Resta da vedere cosa succede per valori di a<1.

 lim k'(cosx)/x^a-3 = 0
 x→0

L’esponente in questo caso è sempre negativo e il limite vale zero.

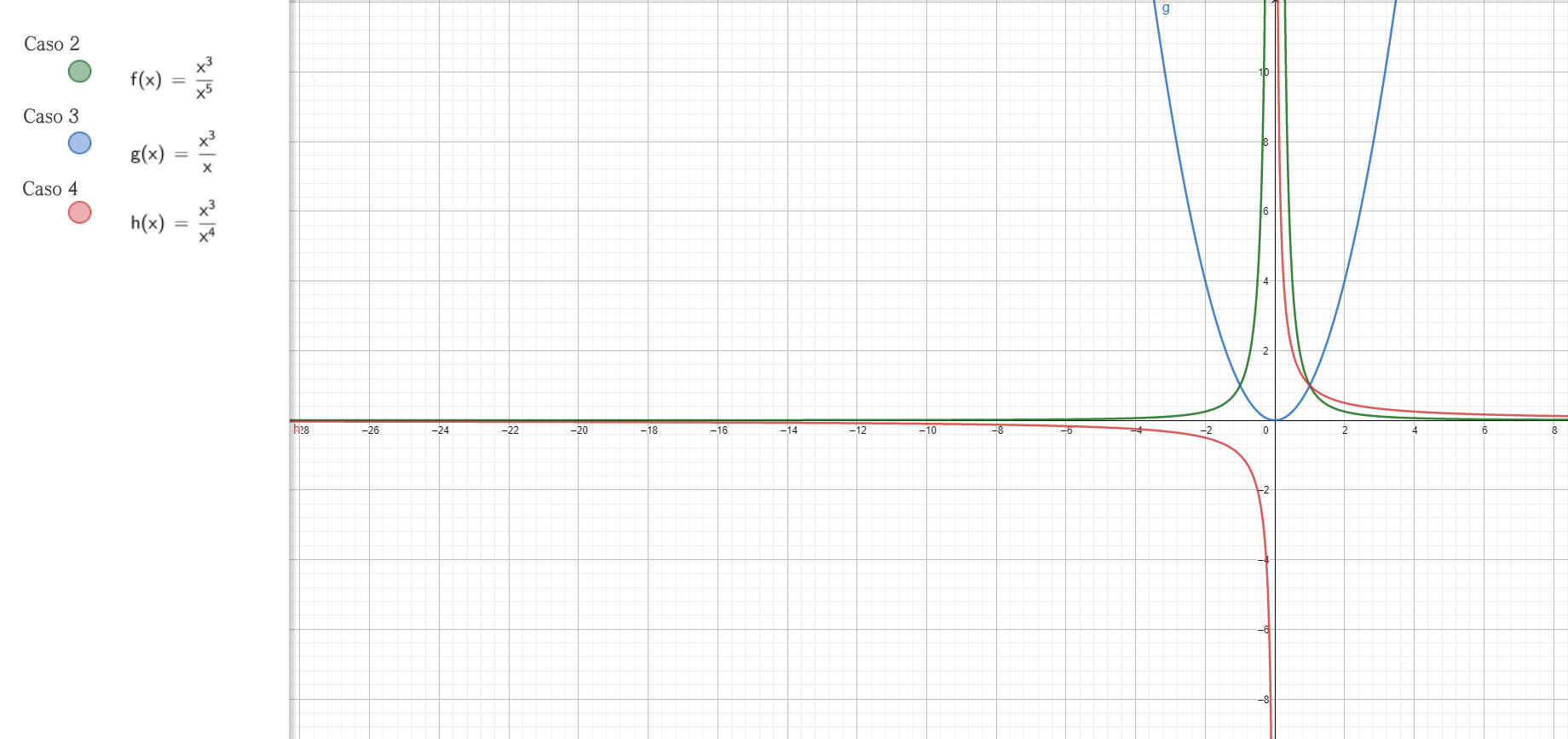
Pertanto l’unico valore che dà limite non nullo e finito è a = 3. In effetti i vari grafici al variare di a della funzione in esame, nell’intorno dello zero, danno ulteriori conferme.

Link per approfondire la prova di maturità scientifica 2017, matematica.

• Vai al Questionario – Quesito 1 – 2017
• Vai al Questionario – Quesito 2 – 2017
• Vai al Questionario – Quesito 3 – 2017
• Vai al Questionario – Quesito 4 – 2017
• Vai al Questionario – Quesito 5 – 2017
• Vai al Questionario – Quesito 6 – 2017
• Vai al Questionario – Quesito 7 – 2017
• Vai al Questionario – Quesito 8 – 2017
• Vai al Questionario – Quesito 9 – 2017
• Vai al Questionario – Quesito 10 – 2017
• Vai al Problema 1 – Quesito 1 – 2017
• Vai al Problema 1 – Quesito 2 – 2017
• Vai al Problema 1 – Quesito 3  – 2017
• Vai al Problema 1 – Quesito 4  – 2017
• Vai al Problema 2 – Quesito 1 – 2017
• Vai al Problema 2 – Quesito 2 – 2017
• Vai al Problema 2 – Quesito 3 – 2017
• Vai al Problema 2 – Quesito 4 – 2017
• Tabella Limiti notevoli
• Regola di de l’Hôpital (Wikipedia)

Random Post

Armadio, armadi – Interpretazione dei sogni

Sognare un armadio, un mobile per i vestiti: interpretazione, significato e numeri associati Il sogno di un armadio è di solito rappresenta i propri pensieri su se stessi. L’abbigliamento che... Vai al post...

PREVISIONE LOTTO n° 130 di VENERDÌ 2 NOVEMBRE 2018

PREVISIONE LOTTO n° 130 di VENERDÌ 2 NOVEMBRE 2018 Esito della previsione precedente: 3)NAZIONALE: Estratto+01-Ambetto. (1) In parentesi tonda, eventuali risultati rilevanti (ambo, terno, ecc) su a... Vai al post...

PREVISIONE LOTTO n° 28 di 150 per GIOVEDI 9 FEBBRAIO 2017

PREVISIONE  LOTTO n° 28 di 150 per GIOVEDI 9 FEBBRAIO 2017 Esito della previsione precedente: BARI:Niente; GENOVA:Niente; PALERMO:Niente; ROMA:Niente. (Nota: è uscito un terno sulla ruota Nazionale... Vai al post...

---

PUBBLICITÀ

---

Disclaimer: Questo blog NON è un prodotto editoriale ai sensi della legge n° 62 del 7 marzo 2001. Le immagini tratte da internet che possano violare i diritti di autore, previa comunicazione, attraverso la sezione -contatti-, verranno prontamente rimosse o sostituite.

Copyright: I contenuti presenti su ROMOLETTO BLOG dei quali è autore il proprietario del blog non possono essere copiati, riprodotti, redistribuiti perché appartenenti all autore stesso. Si vieta la copia e la riproduzione dei contenuti in qualsiasi modo o forma. Si vieta altresì la pubblicazione e la redistribuzione dei contenuti non autorizzata espressamente dell autore.

---

Copyright © 2011 / 2020 - ROMOLETTO BLOG - All Right Reserved

---

Informazioni su Romoletto Blog

Ingegnere Civile, Blogger, Programmatore VB.NET, Lezioni private per scuole medie inferiori e superiori. Per contattarmi scorri la home fino in fondo e vai al form -Contatti-

Visualizza tutti gli articoli di Romoletto Blog →