Analisi Matematica – Paniere Ecampus – AM016-14
Analisi Matematica – Paniere Ecampus – AM016-14
Una serie di problemi e quesiti di Analisi Matematica risolti durante le ripetizioni date a studenti del primo anno di università di varie facoltà di Ingegneria, presi dal paniere Ecampus – Ingegneria Industriale. Analisi Matematica – AM016-14 è un quesito di difficoltà medio-bassa.
Traccia del problema di Analisi Matematica – AM016-14
Se P(x) è un polinomio di grado 3 e Q(x) è un polinomio tale che il limite per x che tende a -∞ di P(x)/Q(x) vale +∞, allora il grado di Q(x):
1) non si può stabilire con le informazioni date;
2) è minore di 4;
3) è maggiore di 4;
4) è uguale a 4.
Soluzione
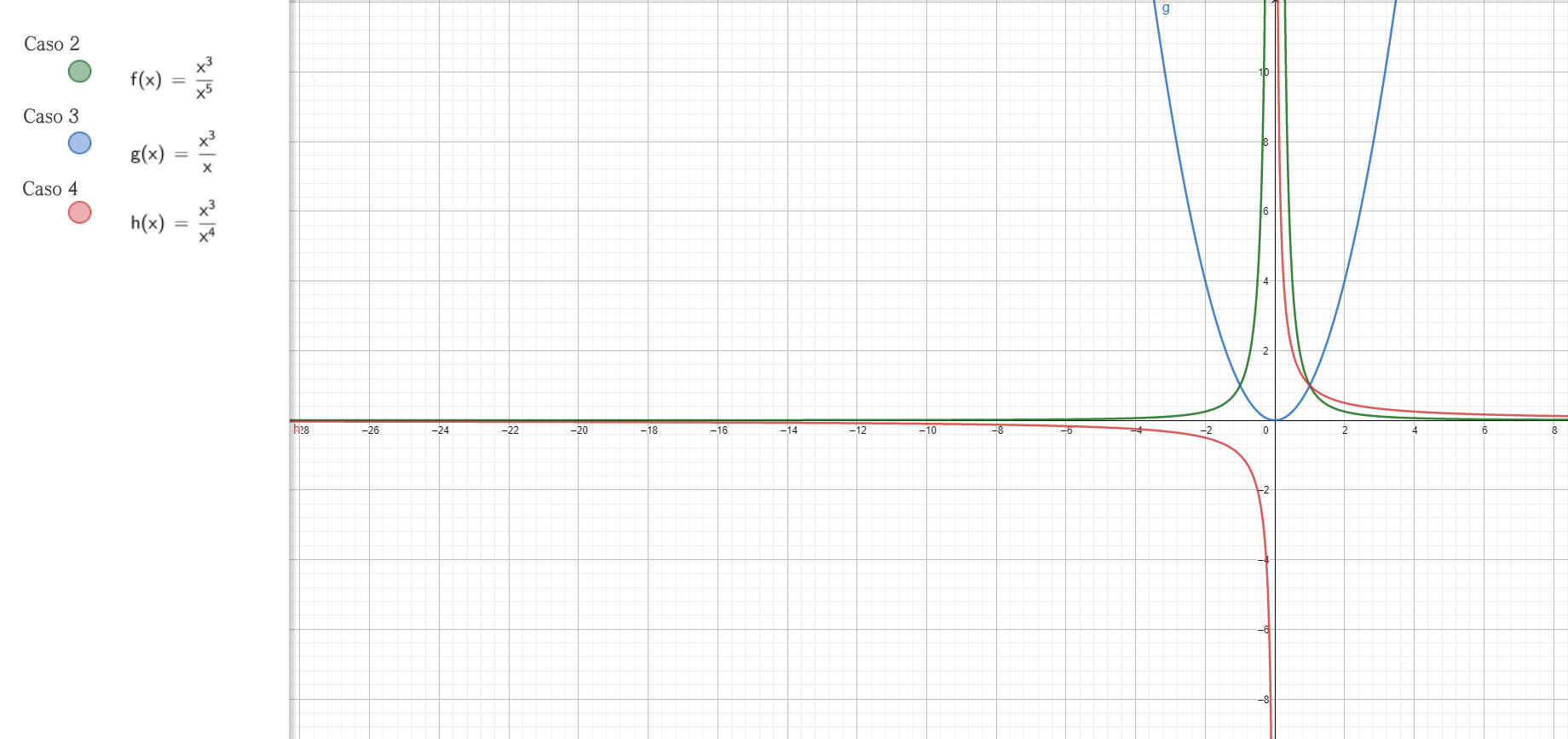
Analisi Matematica – f(x)=(P(x))(Q(x))^-1 – Grafici delle funzioni – AM016-14
Conviene a questo punto ricordarci la regola del confronto tra infiniti. In pratica, specialmente nelle espressioni polinomiali fratte basta trovare, trascurando tutto il resto, i monomi del Numeratore N(x) e del denominatore D(x) a esponente più alto (οmax) ed effettuare il seguente confronto:
- οmax(αN(x)) >οmax(βD(x)) → il limite tende a infinito;
- οmax(αN(x)) =οmax(βD(x)) → il limite tende al rapporto dei coefficienti α/β;
- οmax(αN(x)) <οmax(βD(x)) → il limite tende a zero.
Cerchiamo di analizzare con degli esempi cosa succede, esaminando i vari casi:
\(\lim_{x\rightarrow -\infty}\frac{P(x) }{Q(x)}=+\infty \)- Prendiamo un polinomio P(x) semplicissimo P(x)=x3 e Q(x)=x5 di grado superiore a 4:
\(\lim_{x\rightarrow -\infty}\frac{x^3 }{ x^5 }=+\infty?\)
Poichè siamo nel caso 3 il limite va a zero e quindi lo escludiamo. Ed è cosi per tutti i gradi superiori a 4. - \(\lim_{x\rightarrow -\infty}\frac{x^3 }{ x }=+\infty?\)
In questo caso, siamo nel caso 1, il limite va a infinito positivo, sembrerebbe andare bene. Ma scegliendo un altro denominatore di ordine inferiore a 4 ad esempio:\(\lim_{x\rightarrow -\infty}\frac{x^3 }{ x^2 }=+\infty?\) : il limite va a meno infinito. Quindi già solo per questo non si può considerare corretta. - \(\lim_{x\rightarrow -\infty}\frac{x^3 }{ x^4 }=+\infty?\). Anche in questo caso il limite va a zero, essendo nel caso 3.
Pertanto potremmo sicuramente nessuna delle risposte 2,3 e 4 è vera, e comunque non si può stabilire con le sole informazioni date.
E questo è quanto, salvo errori od omissioni.
Link utili:
- Limite di funzione (Wikipedia)
- UniEcampus (Sito ufficiale)
Elenco AM Ecampus
[el5f806349973d5]