Retta R141 – Problemi di Geometria Analitica
Retta R141 – Problemi di Geometria Analitica.
Una serie di problemi di geometria analitica risolti durante le ripetizioni date a studenti di Liceo Scientifico, Classico e Ragioneria e del primo anno di università di varie facoltà, presi da vari testi scolastici e tracce di compiti in classe. Retta R141 è un problema di difficoltà medio-alta, anche per via del tempo di svolgimento.
[el58862bfc101c9]
Traccia del problema sulla retta R141
Dati i punti A(-1;2) e B(3;6) e la retta r: 2x+3y-17=0 individuare il punto C che essa forma con l’asse del segmento AB e il punto D, nel primo quadrante, tale che ABCD sia un parallelogramma di cui si dovranno determinare il Perimetro e l’Area.
Dati:
A(-1;2) e B(3;6) e la retta r: 2x+3y-17=0
Svolgimento:
Preliminarmente disegniamo il piano cartesiano, fissiamo l’unità di misura e posizioniamo i punti A e B. Disegniamo anche il grafico della retta r.
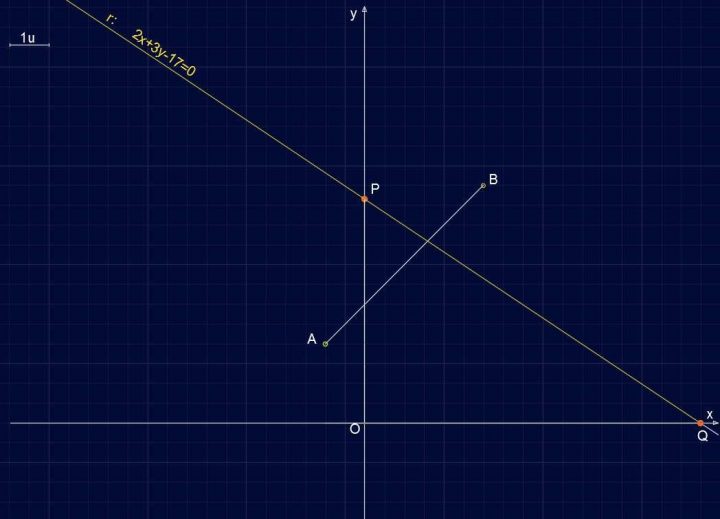
Retta R141 – Piano Cartesiano, punti e retta
Per disegnare il grafico della retta si procede al solito modo, ovvero effettuando l’intersezione con gli assi coordinati e ottenendo i punti P e Q.
Posto:
x=0 ⇒ y=17/3;
y=0 ⇒ x=17/2;
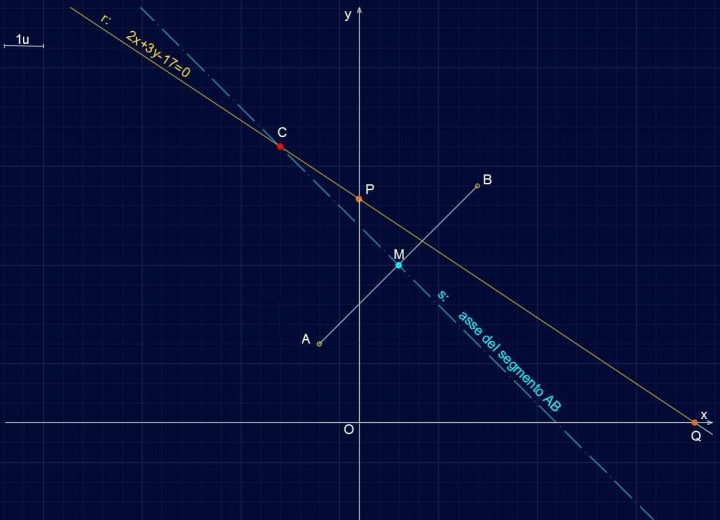
Retta R141 – Asse del segmento, Punto medio M e Punto C
Quindi P(0;17/3) e Q(17/2;0) e da questi punti faremo passare la retta. Dobbiamo ora ricavare l’equazione dell’asse del segmento AB ovvero l’equazione di quella retta passante per il punto medio M di AB e ortogonale al segmento stesso. Determinata tale equazione s: si metterà a sistema con r: in modo da ottenere le coordinate dell’intersezione C.
Posizione di M, punto medio ed equazione dell’asse ‘s’ di AB.
Per ricavare l’equazione dell’asse di AB si procederà mediante l’uso di un fascio di rette proprio con centro in M(xM;yM) e individuando una retta che sia ortogonale a quella passante proprio da A e B. Sfruttando la condizione di ortogonalità tra due rette si deve avere che il coefficiente angolare dell’asse s deve essere l’antireciproco di mAB :
ms = – (mAB)-1
L’equazione del fascio che devo “personalizzare” sarà del tipo:
y-yM = ms(x-xM)
Le coordinate di M(xM;yM) si trovano con le semplici regolette seguenti:
xM = ½(xA+xB) e yM= ½ (yA + yB)
da cui si ottiene, ricordando che A(-1;2) e B(3;6):
xM = ½(-1+3) e yM= ½ (2+6)
xM = 1 e yM= 4
M(1,4)
M rappresenta, come detto, il centro del fascio. Proseguiamo ora andando a ricavare il coefficiente angolare mAB che si ricava dal semplice rapporto:
mAB = (Δy)/(Δx) = (yB – yA)/(xB – xA)
mAB = (6-2)/(3-(-1)) =4/4 = 1
mAB = 1 ⇒ ms = – 1/1 = -1
ms = – 1
Sostituendo tutto si ha:
y-yM = ms(x-xM)
y-4=-1(x-1)
s: x+y-5=0
Per ricavare quindi C si mettono a sistema r: e s:
/ r: 2x+3y-17=0
<
\ s: x+y-5=0
che risolto, ad esempio col metodo di sostituzione, ci da:
/ 10-2y+3y-17=0
<
\ x=5-y
/ y=7
<
\ x=5-y ⇒ x=-2
Il punto è quindi C(-2,7).
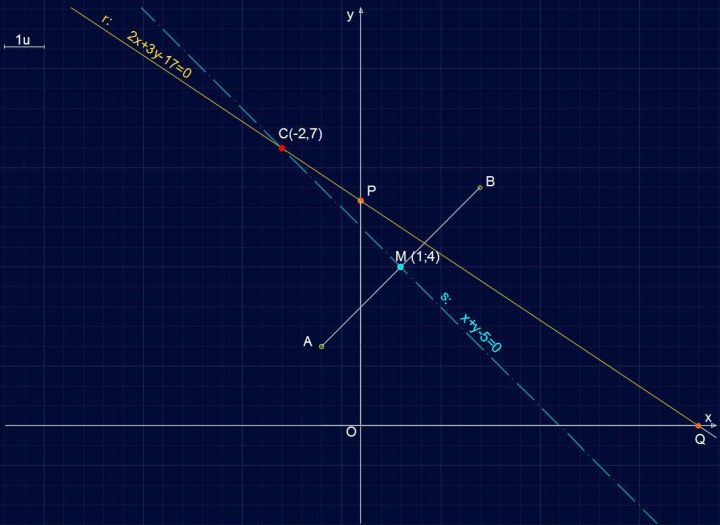
Retta R141 – Risultati Asse del segmento, Punto medio M e Punto C
Posizione del punto D sul primo quadrante
Per determinare il punto D, dobbiamo tenere conto del fatto che un parallelogramma, per definizione, ha i lati opposti a due a due paralleli, per cui una retta passante per CB deve essere parallela a quella passante per AD.
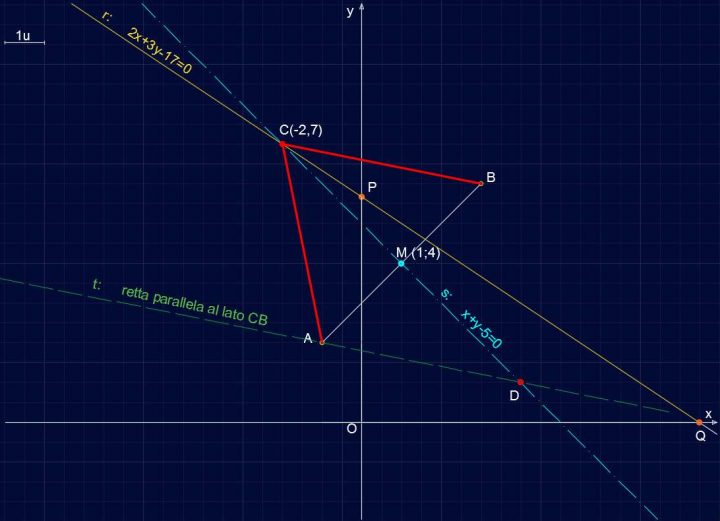
Retta R141 – Retta t e individuazione del punto D
Posizione di D ed equazione della retta ‘t’.
Il procedimento è analogo a quanto fatto nel precedente paragrafo. Per ricavare l’equazione della retta t, passante per A (e D) e parallela a CB si procederà mediante l’uso di un fascio di rette proprio con centro in A(-1;2) e parallela a una retta passante proprio da C e B. Sfruttando la condizione di parallelismo tra due rette si deve avere che il coefficiente angolare della retta t deve essere uguale a quello di mCB :
mt = mCB
L’equazione del fascio che devo “personalizzare” sarà del tipo:
y-yA = mt(x-xA)
si ricava che, ricordando che C(-2,7) e B(3,6):
mCB = (Δy)/(Δx) = (yC – yB)/(xC – xB)
mCB = (7-6)/(-2-3)) = – 1/5
mCB = – 1/5 ⇒ mt = – 1/5
mt = – 1/5
Sostituendo tutto si ha:
y-yA = mt(x-xA)
y-2=-(x+1)/5
t: x+5y-9=0
Per ricavare quindi D si mettono a sistema s: e t:
/ t: x+5y-9=0
<
\ s: x+y-5=0
che risolto, ad esempio col metodo di sostituzione, ci da:
/ 5-y+5y-9=0
<
\ x=5-y
/ y=1
<
\ x=5-y ⇒ x=4
Il punto è quindi D(-4,1). Il nostro parallelogramma è quindi riportato nella figura sottostante.
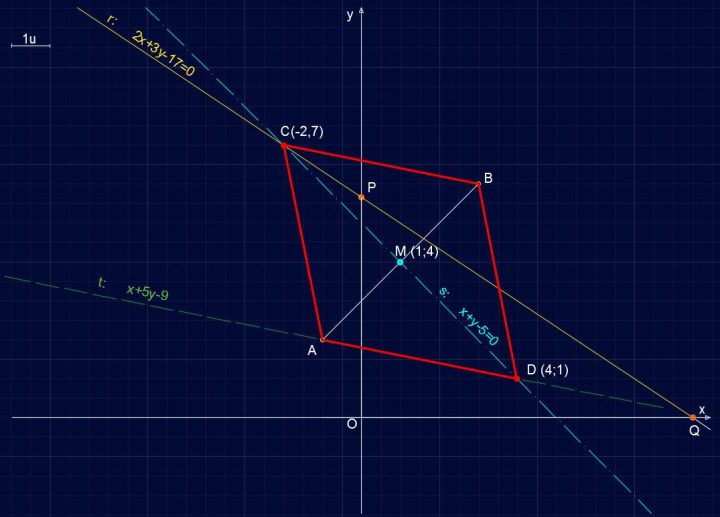
Retta R141 – Individuazione del parallelogramma ABCD
Calcolo di Perimetro e Area del Parallelogramma ABCD
Il calcolo del perimetro è al solito la somma dei lati, per velocizzare il calcolo, poichè CB ≡ AD e CA ≡ BD, esso è dato da
P=2CB+2CA. Quindi:
CB =√((yC – yB)2 + (xC – xB)2)
CB = √((7- 6)2 + (-2 – 3)2) = √26
CA =√((yC – yA)2 + (xC – xA)2)
CA = √((7-2)2 + (-2 + 1)2) = √26
P=2√26+2√26 =4√26.
P=4√26
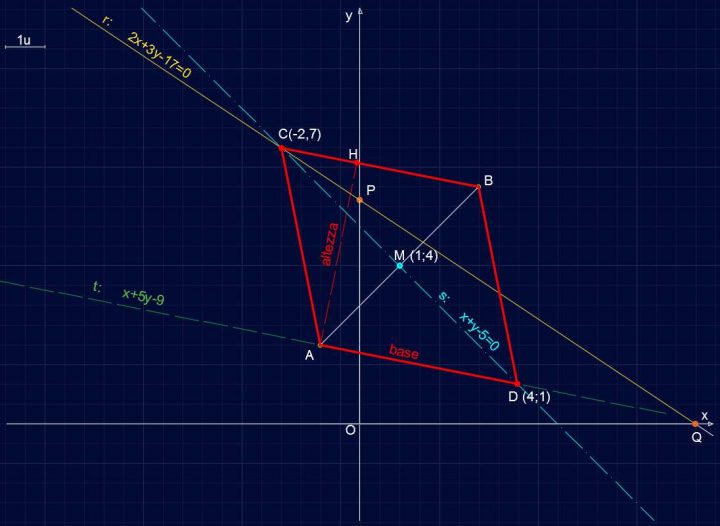
Retta R141 – Perimetro e Area del Parallelogramma ABCD
Il calcolo dell’Area richiede qualche passaggio ulteriore. L’area del parallelogramma è:
A=½ base x altezza
Scegliamo come base AD e l’altezza AH come mostrato in figura. Dobbiamo ricavare l’altezza e lo facciamo usando la formula della distanza punto-retta. In particolare calcoleremo la distanza di C da t (ovviamente CK ≡ AH).
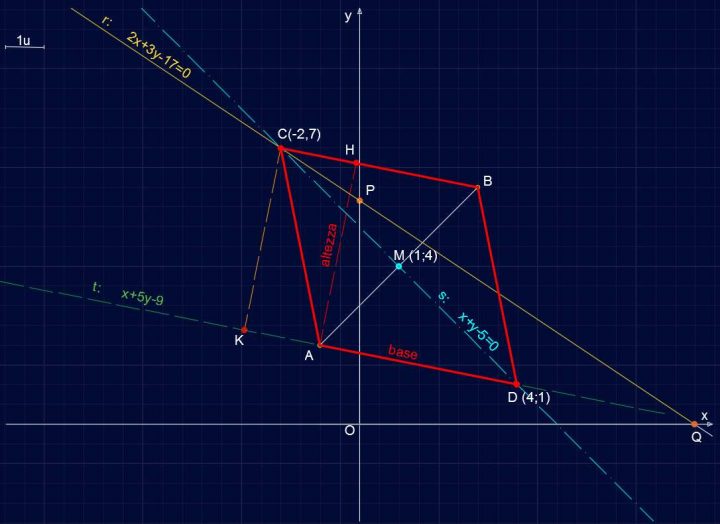
Retta R141 – Altezza del Parallelogramma ABCD
Quindi:
d(C,t)= |atyC + btyC + ct|/√(at2 + bt2)
C(-2,7) e t: x+5y-9=0
d(C,t)= |1*(-2) + 5*7 -9|/√(1 + 25)
d(C,t)= 24/√(26
AH ≡ CK ≡ d(C,t)= 24/√26
Ne consegue che l’Area sarà:
A=½ AD x AH
A=½ √26 x 24/√26 = 12
A = 12
Nota: allo stesso risultato si sarebbe giunti notando che il parallelogramma ABCD in realtà è un rombo (in quanto ha tutti i lati uguali) e perciò:
A=½ Diagonale Maggiore x Diagonale minore
A=½ CD x AB
da calcolare con la formula della distanza tra due punti. E questo è quanto.