Analisi Matematica – Paniere Ecampus – AM016-13
Analisi Matematica – Paniere Ecampus – AM016-13
Una serie di problemi e quesiti di Analisi Matematica risolti durante le ripetizioni date a studenti del primo anno di università di varie facoltà di Ingegneria, presi dal paniere Ecampus – Ingegneria Industriale. Analisi Matematica – AM016-13 è un quesito di difficoltà medio-bassa.
Traccia del problema di Analisi Matematica – AM016-13
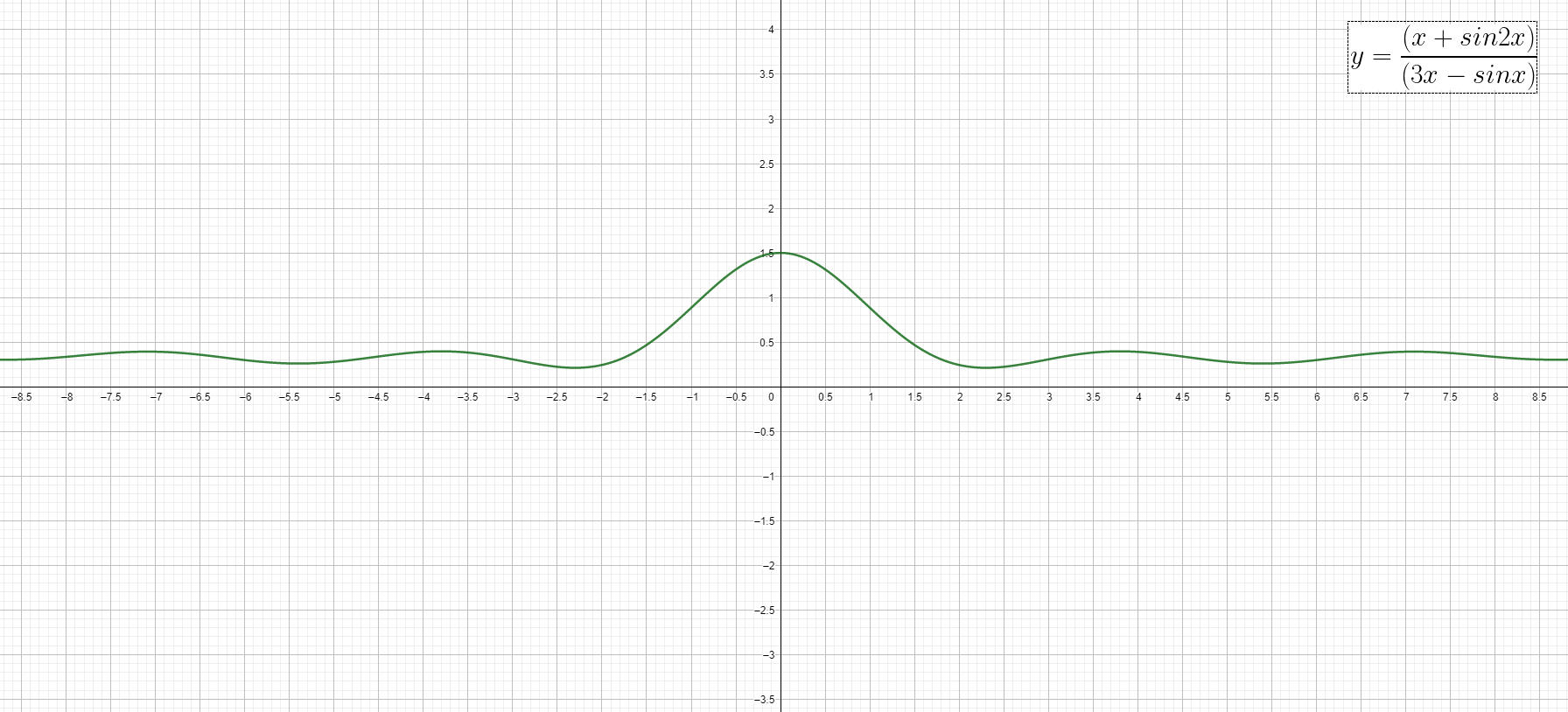
Il limite per x che tende a 0 di (x+sin 2x)/(3x-sin x)
1) vale -2;
2) vale 3/2;
3) vale 1/3;
4) vale -1.
Soluzione
Analisi Matematica – f(x)=(x+sin 2x)(3x-sin x)^-1 – Grafico della funzione – AM016-13
Questo limite ricade, cosi com’è, nella forma indeterminata 0/0:
\(\lim_{x\rightarrow 0}\frac{(x+sin 2x)}{(3x-sin x)}=\frac{0+0}{0-0}=0/0\)
Conviene a questo punto ricordare le regole di approssimazione nell’intorno di x0=0 di Taylor – McLaurin per se funzioni seno e coseno, fermandoci a infinitesimi di ordine superiore a 5 e 4 rispettivamente:
- \( sin(x)=x-\frac{x^{^{3}}}{6}+o(x^{5})\)
- \( cos(x)=1-\frac{x^{2}}{2}+o(x^{4})\)
Nel nostro caso otteniamo:
\( \lim_{x\rightarrow 0}\frac{(x+2x-\frac{8x^{^{3}}}{6}+o(x^{5}))}{(3x-x+\frac{x^{^{3}}}{6}-o(x^{5}))}= \)
\(=\lim_{x\rightarrow 0}\frac{(3x-\frac{8x^{^{3}}}{6}+o(x^{5}))}{(2x+\frac{x^{^{3}}}{6}-o(x^{5}))}= \)Conviene a questo punto ricordarci la regola del confronto tra infinitesimi; in questo caso, sono dello stesso ordine. In pratica, specialmente nelle espressioni polinomiali fratte basta trovare, trascurando tutto il resto, i monomi del Numeratore N(x) e del denominatore D(x) a esponente più basso (οmin) ed effettuare il seguente confronto:
- οmin(αN(x)) <οmin(βD(x)) → il limite tende a infinito;
- οmin(αN(x)) =οmin(βD(x)) → il limite tende al rapporto dei coefficienti α/β;
- οmin(αN(x)) >οmin(βD(x)) → il limite tende a zero.
Nel nostro caso siamo nella situazione al punto 1; i monomi sono infatti:
οminαN(x) = 3x e οminβD(x)=2x;
e possiamo trascurare tutto il resto. I coefficienti sono quindi:
α=3 e β=2.
\(=\lim_{x\rightarrow 0}\frac{3x }{ 2x }=\frac{3}{2} \)E questo è quanto, salvo errori od omissioni.
Link utili:
- Limite di funzione (Wikipedia)
- UniEcampus (Sito ufficiale)
Elenco AM Ecampus
[el5f806349973d5]
