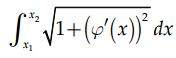Maturità Scientifica 2017 – Problema 1 – Quesito 2
Maturità Scientifica 2017 – Problema 1 – Quesito 2 – Matematica
Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.
[el58862bfc101c9]
Traccia del Problema 1 della Maturità Scientifica 2017 – Quesito 2
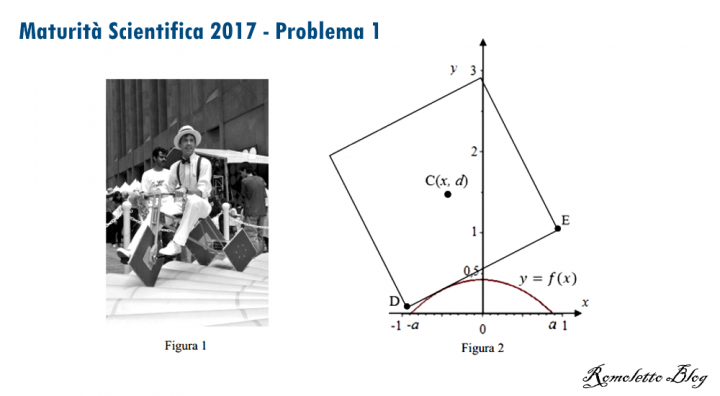
Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New York, al MoMath-Museum of Mathematics si può fare, in uno dei padiglioni dedicati al divertimento matematico (figura 1). È però necessario che il profilo della pedana su cui il lato della ruota può scorrere soddisfi alcuni requisiti. In figura 2 è riportata una rappresentazione della situazione nel piano cartesiano Oxy: il quadrato di lato DE= 2 (in opportune unità di misura) e di centro C rappresenta la ruota della bicicletta, il grafico della funzione f(x) rappresenta il profilo della pedana.
Quesito 2: Perché la bicicletta possa procedere agevolmente sulla pedana è necessario che:
• a sinistra e a destra dei punti di non derivabilità i tratti del grafico siano ortogonali;
• la lunghezza del lato della ruota quadrata risulti pari alla lunghezza di una “gobba”, cioè dell’arco di curva di equazione f(x) per x∈ [−a; a].Stabilisci se tali condizioni sono verificate. *
* In generale, la lunghezza dell’arco di curva avente equazione y =ϕ(x) compreso tra le ascisse x1 e x2 è data da :
Maturità Scientifica 2017 – Problema 1
Svolgimento:
Questo secondo quesito, a prima vista sembrerebbe più abbordabile, se non altro a livello di svolgimento meccanico, in quanto viene fornita una nota con l’integrale da sviluppare. Inoltre si tratta semplicemente di verifiche.
Prima verifica richiesta
Per quanto riguarda la prima verifica, occorre innanzi tutto dire quali sono i punti di non derivabilità (punto angoloso, punto a tangente verticale o punto di cuspide). Per stabilire quali siano, occorrerebbe in generale studiare il campo di esistenza della derivata prima, e gli estremi del CE, ma in questo caso ci si riferisce solo ai punti di ascissa x=-a e x=a; l’unica cosa che potrebbe portare a qualche perplessità è capire al volo cosa significhi che “nei punti di non derivabilità, i tratti del grafico siano ortogonali”: questa frase vuole semplicemente dire che, considerando la Figura 3,
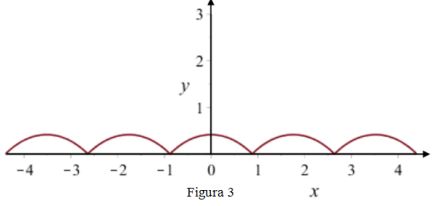
nei punti di unione dei vari spezzoni di curva, l’angolo formato dalla “V” deve essere di 90° ovvero deve essere rispettata la condizione di ortogonalità: f'(-a)+ · f'(a)– = -1 (come per le rette perpendicolari, i cui coefficienti angolari dovevano essere uno l’antireciproco dell’altro).
Quindi : f'(x)= (e-x – ex)/2
e ricordando che:
-a = ln(√2 – 1)≅-0,88
a = ln(√2 + 1)≅0,88
f'(ln(√2 – 1))+ = [1/(√2 – 1)-(√2 – 1)]/2=+1
f'(ln(√2 + 1))– =1/(√2 + 1)-(√2 + 1)]/2=-1
effettivamente è verificato che:
f'(ln(√2 – 1))+ · f'(ln(√2 + 1))– = (1) *(-1)=-1
e quindi i tratti sono perpendicolari. Si può aggiungere anche che si tratta di punti angolosi, in quanto le derivate destra e sinistra pur essendo diverse, sono comunque finite.
Seconda verifica richiesta
Per quanto riguarda la seconda verifica, è molto semplice implementarla: il lato del quadrato vale DE=2, la lunghezza dell’arco di curva si calcola con l’integrale fornito nella nota. Forse è un po’ più complesso svolgerlo. Quindi:
f'(x)= (e-x – ex)/2, pertanto posto:
x1=ln(√2 – 1) e x2=ln(√2 + 1)
x2
∫ √{1+ [(e-x – ex)/2]2} dx = 2
x1
(e-x – ex)2 = e-2x+e2x-2
x2
∫ √{(e-2x+e2x+2)/4} dx =
x1
x2
= ½ ∫ √ (e-2x+e2x+2) dx =
x1
Si pone: t=ex da cui x=ln(t) e dx= dt/t;
inoltre x1=ln(√2 – 1) → t1 = ex1 = (√2 – 1)
e x2=ln(√2 + 1) → t2 = ex2 = (√2 + 1)
t2
= ½ ∫ √ (t -2 +t2+2) dt/t =
t1
t2
= ½ ∫ √ [(t2+1)2/t2 ] dt/t =
t1
t2
= ½ ∫ (t2+1)/t2 dt =
t1
t2
= ½ ∫ 1+ (1/t2 ) dt =
t1
t2 t2
= ½[ ∫ 1· dt + ∫ ( 1/t2 ) dt] =
t1 t1
t2 t2
= ½[ t ] + ½ [ 1/t ] =
t1 t1
= ½[√2 + 1-√2 + 1] + ½[(1/(√2 + 1)) – (1/(√2 – 1))] =
=1 + ½[√2 + 1-√2 + 1] = 1+1=2
e quindi l’uguaglianza imposta è verificata.
Link per approfondire la prova di maturità scientifica 2017, matematica.
- Vai al Questionario – Quesito 1 – 2017
- Vai al Questionario – Quesito 2 – 2017
- Vai al Questionario – Quesito 3 – 2017
- Vai al Questionario – Quesito 4 – 2017
- Vai al Questionario – Quesito 5 – 2017
- Vai al Questionario – Quesito 6 – 2017
- Vai al Questionario – Quesito 7 – 2017
- Vai al Questionario – Quesito 8 – 2017
- Vai al Questionario – Quesito 9 – 2017
- Vai al Questionario – Quesito 10 – 2017
- Vai al Problema 1 – Quesito 1 – 2017
- Vai al Problema 1 – Quesito 2 – 2017
- Vai al Problema 1 – Quesito 3 – 2017
- Vai al Problema 1 – Quesito 4 – 2017
- Vai al Problema 2 – Quesito 1 – 2017
- Vai al Problema 2 – Quesito 2 – 2017
- Vai al Problema 2 – Quesito 3 – 2017
- Vai al Problema 2 – Quesito 4 – 2017
- Pedalare con una bicicletta con le ruote quadrate
- La catenaria (wikipedia)
- Testo della traccia in pdf dal sito Zanicchelli
- Svolgimento della prova su TomwHw.it
- Quaderni di laboratorio 2009 – Una non parabola: la catenaria con qualche cenno al calcolo della sua equazione. Franco Ghione
- L’integrale curvilineo