Maturità Scientifica 2017 – Problema 2 – Quesito 1

by Romoletto Blog · 2 Luglio 2017

Maturità Scientifica 2017 – Problema 2 – Quesito 1 – Matematica

Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.

[el58862bfc101c9]

Traccia del Problema 2 della Maturità Scientifica 2017 – Quesito 1

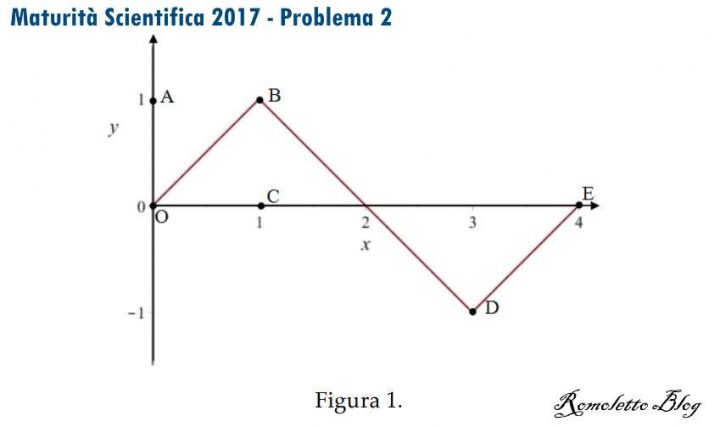
Consideriamo la funzione f : R → R , periodica di periodo T=4 il cui grafico, nell’intervallo [0;4], è il seguente:

Figura 1 Problema 2 Quesito 1 Maturità Scientifica 2017

Romoletto Blog ti consiglia...
Nespresso by De'Longhi Inissia EN80.CW Macchina da caffè, Sistema Capsule Nespresso, Serbatoio acqua 0.7L, Bianco Crema (Cream White)
In omaggio buono da 40€ spendibile sull'acquisto di prodotti nespresso. ...
Nota: prodotto fornito da Amazon

Come si evince dalla Figura 1, i tratti OB, BD, DE del grafico sono segmenti i cui estremi hanno coordinate:

O(0; 0), B(1; 1), D(3; −1), E(4; 0).

Quesito 1: Stabilisci in quali punti del suo insieme di definizione la funzione f è continua e in quali è derivabile e verifica l’esistenza dei limiti:

e
qualora esistano, determinane il valore. Rappresenta inoltre, per x∈ [0;4], i grafici delle funzioni: g(x)= f ′(x) e

Svolgimento:

Il primo quesito di questo secondo problema è abbastanza semplice. Ci chiede di stabilire se è continua e se è derivabile e di dire in quali punti non è possibile fare questo. Inoltre è una funzione periodica, per cui ha sempre l’andamento e caratteristiche, visibili in figura. Sarà perciò sufficiente studiarla in [0,4].

Per prima cosa si osserva che la funzione è costituita da segmenti di rette, per cui ogni segmento avrà la sua retta associata:

L’equazione di una retta passante per 2 punti generici P₀(x₀,y₀) e P₁(x₁,y₁) è data da:

(x-x₀)/(x₁-x₀) = (x-x₀)/(x₁-x₀) oppure y-y₀ =m(x-x₀) con m=(y1-y0)/(x₁-x₀)

r_OB → m=(1-0)/(1-0)=1 → y-0=1(x-0)
r_OB: y = x in [0,1)

r_BD → m=(1+1)/(1-3)=-1 → y-1=-1(x-1)
r_BD: y = 2 – x in [1,3)

r_DE → m=(0+1)/(4-3) = 1 → y+1=1(x-3) D(3; −1), E(4; 0).
r_DE: y = x – 4 in [3,4)

Occorre inoltre osservare che r_OB è un caso “particolare”, in realtà tutte le rette “ascendenti” hanno, vista la periodicità, intersezione con l’asse x (y=0) ogni 4u e perciò saranno del tipo:

y = x – 4k k∈Ζ

Cosicché:

k=0 → y = x → (y=0; x=0)
k=1 → y = x – 4 → (y=0; x=4)
k=2 → y = x – 8 → (x=0; y=8)
… e cosi via …

Stessa cose per le rette “discendenti” che però partono “sfalsate” di 2u e si ripetono sempre ogni 4u :

y = 4k – x +2 = 2(2k+1)-x k∈Ζ

Cosicché:

k=0 → y = 2 – x → (y=0; x=2)
k=1 → y = 4 – x + 2 → (y=0; x=6)
k=2 → y = 8 – x + 2 → (x=0; y=10)
… e cosi via …

La funzione può essere cosi scritta, tenendo conto di k e degli intervalli , su tutto R, come:

/ x – 4k se x ∈ [4k,4k+1) ∪ [4k+3,4k+1+3)
f(x)= <
\ 2(2k+1)-x se x ∈ [4k+1,4k+3)

con k∈Ζ.

Questa funzione è continua a tratti (i segmenti sono porzioni di retta, che è continua); gli unici punti da tenere d’occhio sono quelli di cresta e cavo e a ogni “giunzione” di periodo T=4k (k∈Ζ): basta però effettuare il limite destro e sinistro per vedere come essi coincidano e coincidano inoltre con il valore di f(x) in quei punti:

(giuzione)
lim f(x) = 4k-4k = 0 =f(4k)
x → 4k^–
lim f(x) = 4k-4k = 0 =f(4k)
x → 4k⁺

(cresta)
lim f(x) = 4k+1-4k= 1 = f(4k+1)
x → (4k+1)^–
lim f(x) = 2(2k+1)-(4k+1) =1 =f(4k+1)
x → (4k+1)⁺

(cavo)
lim f(x) = 2(2k+1)-(4k+3)=-1= f(4k+3)
x → (4k+3)^–
lim f(x) = (4k+3)-4(k+1)*=-1= f(4k+3)
x → (4k+3)⁺

*Nota: si è messo (k+1) e non k perchè mentre la prima retta di sinistra (che passa per x=3) si costruisce con k=0, quella a destra invece, sempre passante per x=3 si costruisce con k successivo (k+1 appunto). Se si fosse lasciato k e quindi x-4, si sarebbe considerata la retta passante per l’origine.

La funzione è dunque continua in tutto R.

Vediamo la derivabilità. Poichè si tratta di spezzoni di rette, questi sono derivabili sempre. Le uniche perplessità potrebbero esserci al solito nei punti di cresta cavo e di “giunzione” dei vari tratti in genere. Deriviamo:

/ 1 se x ∈ [4k,4k+1) ∪ [4k+3,4k+1+3)
f'(x)= <
\ -1 se x ∈ [4k+1,4k+3)

con k∈Ζ

La derivata è costituita quindi da costanti. Al solito controlliamo se a destra e a sinistra i valori coincidono:

(giuzione)
f'(4k)⁺= 1 = f'(4k)^–
Negli zeri, la funzione è continua e derivabile.

(cresta)
f'(4k+1)⁺= -1
f'(4k+1)^–= 1
Le derivate sono finite, ma diverse: è un punto di non derivabilità (punto angoloso). Quindi in tutti i punti del tipo x=4k+1 (k∈Z) non è derivabile.

(cavo)
f'(4k+1)⁺= 1
f'(4k+1)^– = -1
Le derivate sono finite, ma diverse: è un punto di non derivabilità (punto angoloso). Quindi in tutti i punti del tipo x=4k+3 (k∈Z) non è derivabile.

La funzione non è derivabile nei punti di ascissa: x=4k+1 e x=4k+3 (k∈Z).

Il quesito ci chiede poi di controllare anche il comportamento all’infinito della funzione:

Si può rispondere subito dicendo che di una funzione periodica non si può stabilire a quale valore tende all’infinito e quindi non esiste.

Studiamo anche il limite:

La funzione diventa quindi:

/ (x – 4k)/x se x ∈ [4k,4k+1) ∪ [4k+3,4k+1+3)
f(x)= <
\ (2(2k+1) -x )/x se x ∈ [4k+1,4k+3)

Poiché dobbiamo studiare il comportamento all’infinito anche k → ∞, tuttavia anche se x o k diventano immensamente grandi, il valore di f(x), per come è definita, è compreso sempre tra [-1,1], e quindi è un valore finito; pertanto il quoziente di un numero finito fratto infinito, tenderà a zero.

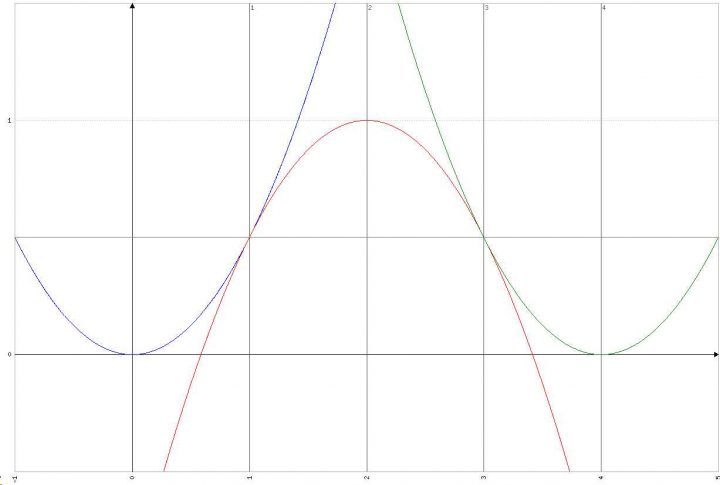
Per quanto riguarda il grafico della g(x)=f'(x) in [0;4] è semplicissimo:

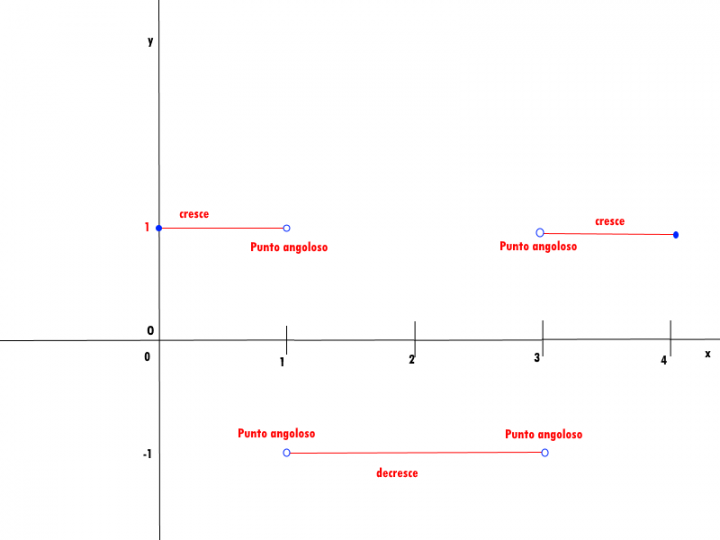
Grafico Derivata Problema 2 Quesito 1 Maturità Scientifica 2017

Per quanto riguarda il grafico della funzione integrale, nell’intervallo [0,4]:

per definizione esso rappresenta l’area sottesa dalla funzione; essendo 2 triangoli isosceli, sommandoli è come avere un quadrato di lato l=√2 e quindi di area 2. Proviamolo anche analiticamente, ricordando che il risultato dell’integrale di ogni intervallino considerato deve essere sommato al precedente, per avere l’andamento reale della funzione h(x).

x∈[0,1); k=0
x x 1
h(x)=∫ t dt = [½t²] = ½x² → [ ½x²] = ½
0 0 0

x∈[1,3); k=0
x x
h(x)= ½ + ∫ (2-t) dt = [2t – ½t²] =
1 1
= ½ +(2x – ½x² – 2 + ½) =
= 2x – ½x² – 1

3
[2x – ½x² – 1] =6-(9/2)-1 = ½
0

x∈[3,4); k=1
x x
h(x)=½ +∫ (t-4) dt = [½t²– 4t] =
3 3

= ½ + (½x²– 4x – (9/2)+12 ) =
= [½x² – 4x + 8]

Sono tutti archi di parabola: