Maturità Scientifica 2017 – Questionario – Quesito 10 – Matematica

Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.

Traccia del Quesito 10 del Questionario Maturità Scientifica 2017

Data la funzione: f(x)=|4−x²|, verificare che essa non soddisfa tutte le ipotesi del Teorema di Rolle nell’ intervallo [−3; 3] e che comunque esiste almeno un punto dell’intervallo [−3; 3] in cui la derivata prima di f(x) si annulla. Questo esempio contraddice il Teorema di Rolle? Motivare la risposta in maniera esauriente.

Maturità Scientifica 2017 – Questionario – Quesito 10

Svolgimento:

Questo decimo e finalmente ultimo quesito del questionario della maturità scientifica 2017 è, come il nono, quasi esclusivamente teorico e richiede di verificare le ipotesi del Teorema di Rolle.

Il teorema di Rolle

Se una funzione f(x) e’ continua in un intervallo chiuso e  limitato [a,b] ed è ivi derivabile e se inoltre agli estremi dell’intervallo funzione assume lo stesso valore f(a)=f(b) allora esiste almeno un punto dell’intervallo in cui la derivata della funzione è nulla.

Quindi le ipotesi da verificare sono:

1. La funzione deve essere continua in [a,b];
2. L’intervallo [a,b] deve essere chiuso e limitato;
3. I valori agli estremi devono essere uguali: f(a)=f(b);
4. La funzione deve essere derivabile in (a,b).

Scriviamo in modo più esplicito la funzione f(x) che è data da:

1. se -2≤x≤2 cioè x∈[-2,2] → f(x)=4-x²
2. se x>2 o x<-2 cioè x∈[-3,-2) o x∈(2,3] → f(x)=x²-4

che rappresentiamo graficamente qui di seguito.

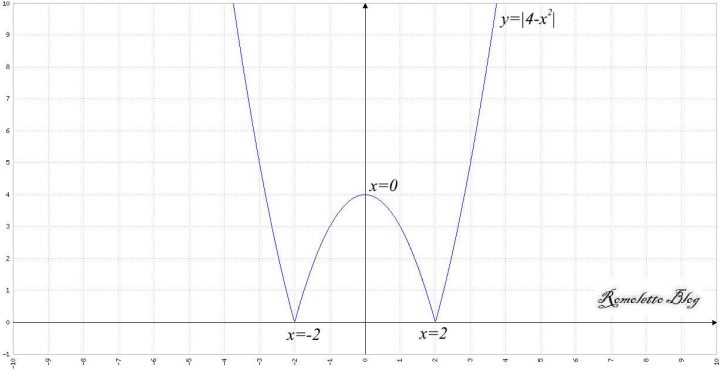
Grafico della funzione – Maturità Scientifica 2017 – Questionario – Quesito 10

Verifichiamo:

1. La funzione f(x)=|4−x²| non presenta punti di discontinuità, perciò è continua. Indaghiamo per scrupolo nel punto in  x=2 e in x=-2 controllando che sia il limite destro che quello sinistro siano rispettivamente uguali.
   lim |4−x²| = 0
   x→-2⁺
   lim |4−x²| = 0
   x→-2^–
   Non è un punto di discontinuità;   lim |4−x²| = 0
   x→2⁺
   lim |4−x²| = 0
   x→2^–
   Non è un punto di discontinuità. OK
2. L’intervallo [-3,3] è chiuso, ed è sicuramente limitato in quanto sottoinsieme chiuso di R, dominio di f(x). OK
3. f(-3)=f(3)=5. OK
4. La funzione nell’intervallo (-3,3) non è derivabile: infatti in x=-2 e x=2, punto in cui f(x)=0, abbiamo un punto angoloso ovvero un punto di non derivabilità in quanto, pur esistendo finite entrambe, la derivata destra è diversa dalla derivata sinistra (o meglio: il limite da destra della derivata destra è diverso dal limite da sinistra della derivata sinistra). Calcoliamo la derivata di f(x):
   a) f'(x)=-2x
   b) f'(x)=+2x
   quindi:
   lim -2x = 4
   x→-2⁺
   lim 2x = -4
   x→-2^–
   E’ un punto angoloso;lim -2x = -4
   x→2⁺
   lim  2x = 4
   x→2^–
   E’ un punto angoloso.
   Pertanto l’ipotesi di derivabilità non è rispettata. NO.

Poichè la funzione non rispetta la condizione di derivabilità in tutto l’intervallo (-3;3), allora non si può applicare Rolle.

Per quanto riguarda la seconda questione, il punto in cui la derivata prima si annulla lo possiamo calcolare in questo modo. Ricordando che f(x) è data da:

1. se -2≤x≤2 cioè x∈[-2,2] → f(x)=4-x²
2. se x>2 o x<2 cioè x∈[-3,2) o x∈[2,3] → f(x)=x²-4

e che la sua derivata è, rispettivamente:

1. f'(x)=-2x
2. f'(x)=+2x

In entrambi i casi si annulla per x=0. Quindi pur non rispettando le ipotesi di Rolle, abbiamo trovato un punto in cui la derivata prima si annulla. Questo non contraddice il teorema in quanto, appunto, non è detto che se si ha una derivata nulla allora la funzione è derivabile (come se fosse una condizione di derivabilità). Rolle non pone una condizione necessaria e sufficiente ( ⇔ ) ma solo la condizione sufficiente( ⇒ ).

Link per approfondire la prova di maturità scientifica 2017, matematica.

• Vai al Questionario – Quesito 1 – 2017
• Vai al Questionario – Quesito 2 – 2017
• Vai al Questionario – Quesito 3 – 2017
• Vai al Questionario – Quesito 4 – 2017
• Vai al Questionario – Quesito 5 – 2017
• Vai al Questionario – Quesito 6 – 2017
• Vai al Questionario – Quesito 7 – 2017
• Vai al Questionario – Quesito 8 – 2017
• Vai al Questionario – Quesito 9 – 2017
• Vai al Questionario – Quesito 10 – 2017
• Vai al Problema 1 – Quesito 1 – 2017
• Vai al Problema 1 – Quesito 2 – 2017
• Vai al Problema 1 – Quesito 3  – 2017
• Vai al Problema 1 – Quesito 4  – 2017
• Vai al Problema 2 – Quesito 1 – 2017
• Vai al Problema 2 – Quesito 2 – 2017
• Vai al Problema 2 – Quesito 3 – 2017
• Vai al Problema 2 – Quesito 4 – 2017
• Il teorema di Rolle (Wikipedia)

Random Post

PREVISIONE LOTTO n° 76 di 150 per GIOVEDÌ 1 GIUGNO 2017

PREVISIONE LOTTO n° 76 di 150 per GIOVEDÌ 1 GIUGNO 2017 Esito della previsione precedente: 1)BARI: Estratto; 5)PALERMO: Estratto + 1 ambetto; E|FIRENZE: 1euro; G|TORINO: 1euro. Previsione “bet... Vai al post...

PREVISIONE LOTTO n° 122 di SABATO 13 OTTOBRE 2018

PREVISIONE LOTTO n° 122 di SABATO 13 OTTOBRE 2018 Esito della previsione precedente: 1)CAGLIARI: 1 euro 10eLotto; 2)BARI: Niente; (TERNO RM). (1) In parentesi tonda, eventuali risultati rilevanti (... Vai al post...

PREVISIONE LOTTO n° 132 di MARTEDÌ 6 NOVEMBRE 2018

PREVISIONE LOTTO n° 132 di MARTEDÌ 6 NOVEMBRE 2018 Esito della previsione precedente: 2)FIRENZE: Estratto; 3)ROMA: 10 euro 10eLotto;(Ambo BA; Ambo NA; Ambo NZ); 4)BARI: Estratto. (1) In parentesi ... Vai al post...

---

PUBBLICITÀ

---

Disclaimer: Questo blog NON è un prodotto editoriale ai sensi della legge n° 62 del 7 marzo 2001. Le immagini tratte da internet che possano violare i diritti di autore, previa comunicazione, attraverso la sezione -contatti-, verranno prontamente rimosse o sostituite.

Copyright: I contenuti presenti su ROMOLETTO BLOG dei quali è autore il proprietario del blog non possono essere copiati, riprodotti, redistribuiti perché appartenenti all autore stesso. Si vieta la copia e la riproduzione dei contenuti in qualsiasi modo o forma. Si vieta altresì la pubblicazione e la redistribuzione dei contenuti non autorizzata espressamente dell autore.

---

Copyright © 2011 / 2020 - ROMOLETTO BLOG - All Right Reserved

---

Informazioni su Romoletto Blog

Ingegnere Civile, Blogger, Programmatore VB.NET, Lezioni private per scuole medie inferiori e superiori. Per contattarmi scorri la home fino in fondo e vai al form -Contatti-

Visualizza tutti gli articoli di Romoletto Blog →