Studio di Funzione SF005 – Analisi Matematica
Studio di Funzione SF005 – Analisi Matematica.
Una serie di studi di funzione di Analisi Matematica svolti per gli studenti dell’ultimo anno di Scuola Superiore o per il primo anno di Università, presi dalle ripetizioni date a studenti di Liceo Scientifico e a matricole universitarie. Studio di Funzione SF005 è di difficoltà bassa, ma completo di tutti i passaggi.
[el58862bfc101c9]
Traccia dello Studio di Funzione SF005
Studiare la funzione:
y = (3x2+5x-4)/(x-1)
e disegnarne il grafico.
Svolgimento:
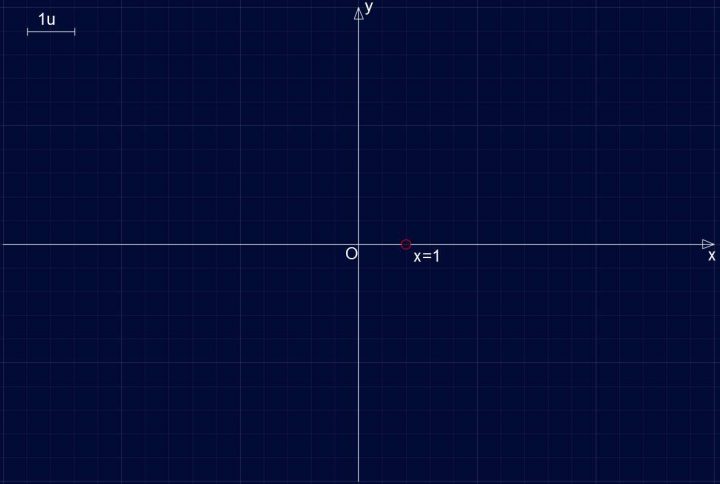
Lo svolgimento dello studio di funzione è alquanto standardizzato. I passi da seguire sono bene o male sempre gli stessi. Si disegna un sistema di riferimento Oxy cartesiano e si fissa l’unità.
Si procede inizialmente a determinare il Campo di Esistenza della funzione che è dato, nel nostro caso, dal porre il denominatore D(x)≠0 diverso da zero → x-1 ≠ 0 → x≠1
Quindi si ha il C.E. = {∀x∈R / x≠1}.
Con lo studio del Campo di Esistenza possiamo iniziare a togliere dal grafico le eventuali parti in cui non dovremo disegnare la funzione. In questo caso dobbiamo eliminare ‘purtroppo’ solo il punto di ascissa x=1.
Uno studio che potrebbe essere utile a ottimizzare i tempi è quello della simmetria rispetto all’ asse Y o rispetto all’origine O. Se una funzione è simmetrica in tal senso, basta studiarne metà in quanto l’altra metà è identica e “specchiata”.
Per quanto riguarda la simmetria rispetto all’asse y, si deve verificare che f(x)=f(-x). Nel nostro caso: f(x)=(3x2+5x-4)/(x-1); f(-x)=(3(-x)2+5(-x)-4)/((-x)-1) pertanto si ottiene che [(3x2+5x-4)/(x-1)] ≠ [(3x2-5x-4)/(-x-1)]; ovvero non è simmetrica rispetto all’asse y.
Per quanto riguarda la simmetria rispetto all’origine O, si deve invece verificare che f(x)=-f(-x). Nel nostro caso f(x)=(3x2+5x-4)/(x-1); -f(-x)=-(3(-x)2+5(-x)-4)/((-x)-1) pertanto si ottiene che [(3x2+5x-4)/(x-1)] ≠ [(3x2-5x-4)/(x+1)]; ovvero non è simmetrica rispetto all’origine O.
Adesso si passa a determinare, se esistono, i punti di intersezione della funzione con gli assi coordinati e allo studio della positività o negatività della funzione. Ricordiamo che “intersezione” equivale a dire “sistema”, in particolare se ne studiano due: uno tra funzione e asse delle ascisse, uno tra funzione e asse delle ordinate.
Intersezione con l’asse Y: il sistema è tra A) x=0 e B) y = (3x2+5x-4)/(x-1) che si risolve istantaneamente sostituendo A) in B) ottenendo cosi: y = 4. Pertanto il primo punto di intersezione è P(0,4).
Intersezione con l’asse X: il sistema è tra A) y=0 e B) y = (3x2+5x-4)/(x-1) che si risolve quindi sostituendo A) in B) ottenendo cosi: 0 = (3x2+5x-4)/(x-1) ovvero (3x2+5x-4)/(x-1) = 0, che è un’equazione fratta. Ricordiamo che per risolvere un’equazione fratta basta che sia il Numeratore N(x)=0, pertanto dobbiamo cercare le soluzioni di (3x2+5x-4)=0. Si tratta di un’equazione di secondo grado completa del tipo ax2+by+c=0; pertanto calcoliamo subito il discriminante Δ=b2-4ac. Otteniamo Δ=25+48=73; Δ>0 il che ci garantisce due soluzioni reali e distinte. Le radici quindi (vedi la Simple Apps per ricavarle online), le troviamo con la solita formuletta:
x1,2 = (-b±√Δ)/(2a) da cui:
x1 = (-5-√73)/6 ≅ -2.3 e
x2= (-5+√73)/6 ≅ 0.6
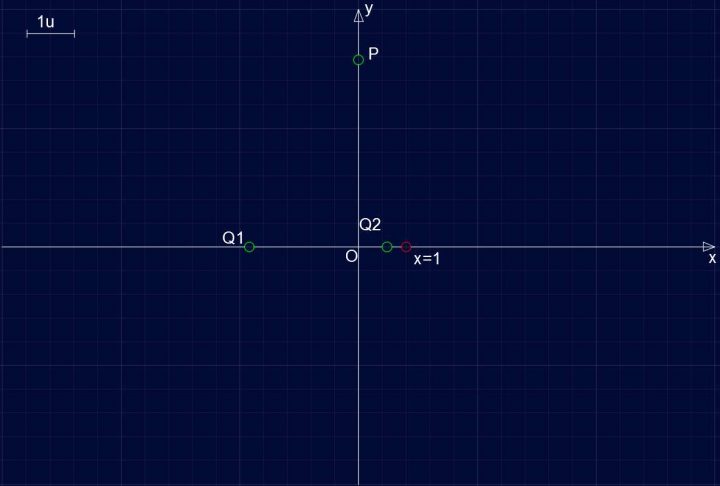
Si sono calcolate numericamente le radici per avere un’idea esatta su dove posizionare tali valori nel grafico. Si ottengono i punti Q1((-5-√73)/6 , 0) e Q2( (-5+√73)/6, 0). Ricapitolando abbiamo tre punti di intersezione:
P(0,4), Q1((-5-√73)/6 , 0) e Q2( (-5+√73)/6, 0) che approssimiamo a ∼P(0,4), ∼Q1(-2.3,0) e ∼Q2(0.6,0) e li rappresentiamo.
I calcoli appena effettuati ci servono per il passaggio successivo, ovvero studio della positività. Dobbiamo porre f(x)>0 cioè [(3x2+5x-4)/(x-1)]>0. Quindi dobbiamo studiare il segno della disequazione fratta, studiando separatamente la disequazione Numeratore N(x)>0 e quella Denominatore D(x)>0, mettendo a grafico gli intervalli ed effettuando il prodotto dei segni.
A) N(x)>0 → 3x2+5x-4>0
Le radici le abbiamo trovate poco fa:
x1 = (-5-√73)/6 ≅ -2.3 e
x2= (-5+√73)/6 ≅ 0.6; ed è Δ>0 e a>0.
Quindi la soluzione è per valori esterni:
N(x)>0 ⇔ {∀x∈R / x< (-5-√73)/6 ∧ x>(-5+√73)/6}.
B) D(x)>0 → x-1>0 che banalmente fornisce x>1.
Effettuiamo lo studio del segno della disequazione fratta:
Valori: x1 0 x2 1
N(x)>0 : + +)- – – -(+ + + + +
D(x)>0 : – – – – – – – – (+ +
Segno : – ( + ) – )1( +
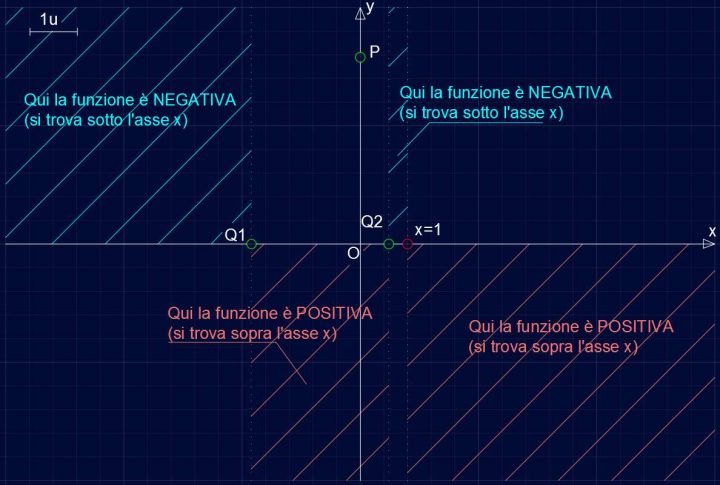
Otteniamo quindi che la funzione è positiva nell’intervallo seguente:
f(x)>0 ⇔ {∀x∈R/(-5-√73)/6<x<(-5+√73)/6 ∧ x>1}.
Questo ci permette di “eliminare” le parti del piano cartesiano in cui non passa la funzione.
Il passo successivo consiste nello studiare l’andamento della funzione in punti particolari (discontinuità, agli estremi del campo di esistenza, ecc), cioè verificando la presenza di asintoti verticali, orizzontali o obliqui.
Gli asintoti verticali si trovano in corrispondenza dei punti di discontinuità, dei “buchi” del dominio, ai limiti del campo di esistenza; nel nostro caso si deve studiare cosa accade nell’intorno di x=1. Se la funzione tende a infinito allora si ha un asintoto verticale.
Se : lim f(x) = ∞ → ∃ asintoto verticale
x→c
Entriamo nel merito della questione studiando:
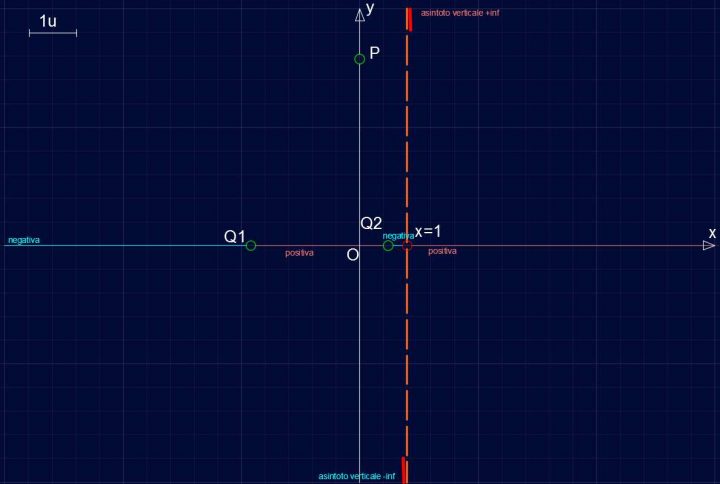
lim [(3x2+5x-4)/(x-1)]= 4/0– = -∞
x→1–
(Asintoto verticale sinistro)
lim [(3x2+5x-4)/(x-1)]= 4/0+ = +∞
x→1+
(Asintoto verticale destro).
Entrambi tendono a infinito, quindi la retta verticale di equazione x=1 è un asintoto verticale. A sinistra la funzione scende fino a meno infinito, a destra sale fino a più infinito. Questo conferma lo studio del segno della funzione: a destra di x=1 infatti è positiva, a sinistra è negativa.
Studiamo ora gli asintoti orizzontali che si ottengono dallo studio del comportamento della funzione all’infinito; se tende a un valore finito allora si ha l’asintoto cercato.
Se : lim f(x) = k → ∃ asintoto orizzontale
x→∞
Ma traduciamo in linguaggio matematico.
lim [(3x2+5x-4)/(x-1)]= (∞/∞)
x→ -∞
lim [(x2(3+(5/x)-(4/x2))/(x(1-(1/x))]= -∞
x→ -∞
(Non abbiamo asintoto orizzontale sinistro)
lim [(3x2+5x-4)/(x-1)]= (∞/∞)
x→ +∞
lim [(x2(3+(5/x)-(4/x2))/(x(1-(1/x))]= +∞
x→ +∞
(Non abbiamo asintoto orizzontale destro)
Non otteniamo asintoti orizzontali, in quanto i limiti non tendono a valori finiti. Notare che se avessimo trovato asintoti orizzontali non sarebbe stato necessario studiare gli asintoti obliqui (per lo meno ognuno nel suo semipiano).
Dobbiamo perciò procedere alla ricerca degli asintoti obliqui; poiché l’asintoto è semplicemente una retta e questa la si esprime attraverso la forma esplicita y=mx+q, allora occorre determinare il coefficiente angolare m e q intersezione con l’asse y. Anche in questo caso si tratta di uno studio al limite, che deve fornire valori finiti.
m = lim f(x)/x = k valore finito
x→∞
q = lim f(x) – mx = j valore finito
x→∞
In particolare, per la nostra funzione si ha:
msx = mdx = lim [(3x2+5x-4)/(x-1)]/x =
x→ ±∞
= lim [(3x2+5x-4)/(x2-x)] = (∞/∞) =
x→ ±∞
= lim [(x2(3+(5/x)-(4/x2)))/(x2(1-(1/x))] = 3
x→ ±∞
Abbiamo il coefficiente angolare m=3. Cerchiamo q.
q = lim [(3x2+5x-4)/(x-1)] – 3x =
x→∞
= lim [(3x2+5x-4 –3x2+3x)/(x-1)] =
x→∞
= lim [(x(8-(4/x))/(x(1-(1/x))] = 8
x→∞
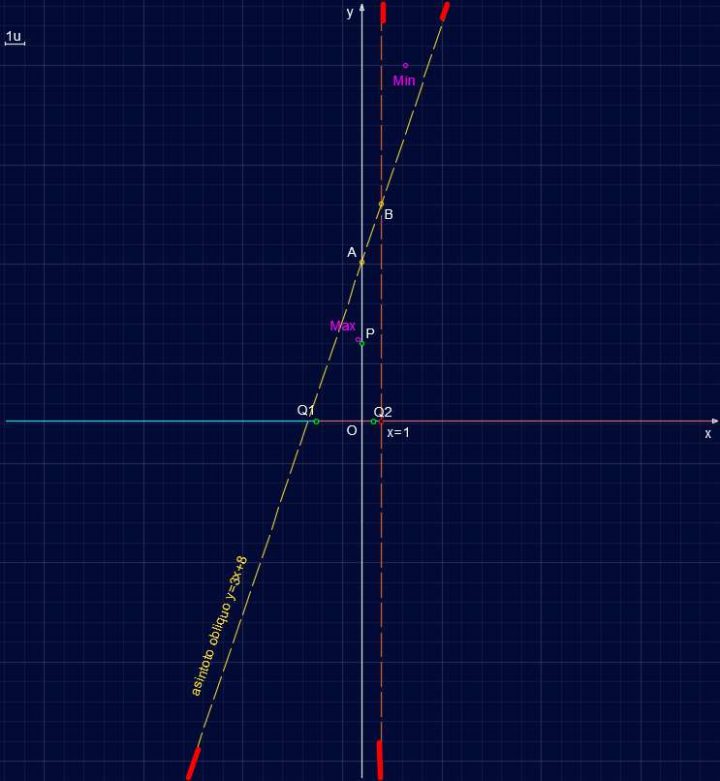
Abbiamo l’intersezione con l’asse delle ordinate, q=8. L’asintoto obliquo quindi esiste ed è la retta:
y = 3x+8
che possiamo rappresentare calcolando due punti ad esempio:
x=0 → y=8 → A(0,8) e x=1 → y=11 → B(1,11).
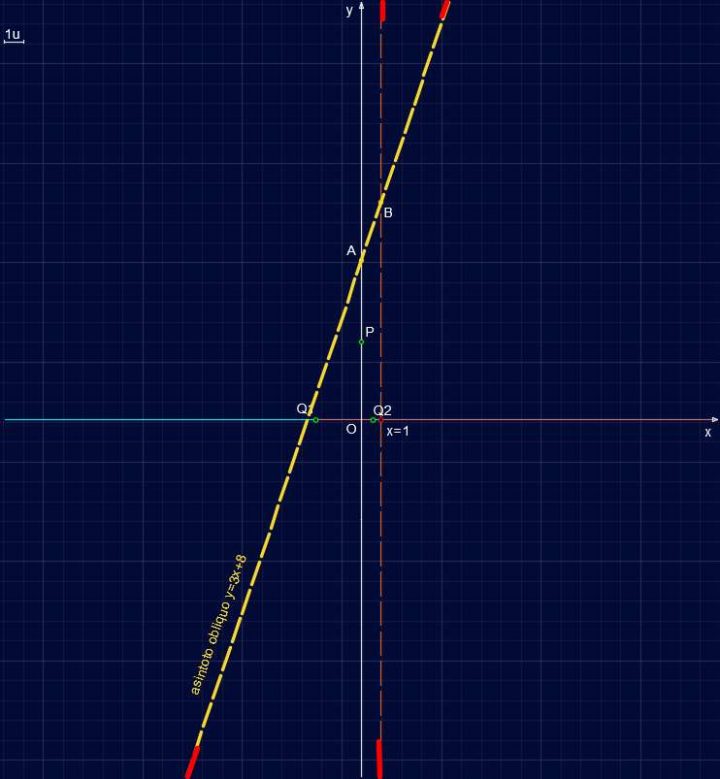
Studio di Funzione SF005 – Asintoto obliquo
Proseguiamo con lo studio di massimi e minimi e crescenza e decrescenza della funzione. In particolare massimi o minimi si trovano ponendo a zero la derivata prima f'(x)=0. Quindi:
f(x)=(3x2+5x-4)/(x-1) → f'(x)=? è una funzione fratta quindi:
f'(x)=(N(x)/D(x))’ = (N'(x)D(x)-N(x)D'(x))/(D(x))2
N'(x)=(6x+5); D'(x)=1; sostituendo:
f'(x)=((6x+5)(x-1)-(3x2+5x-4)(1))/(x-1)2 =
= (6x2-6x+5x-5-3x2–5x+4=
= (3x2 – 6x – 1)/(x-1)2
quindi si studia solo: 3x2-6x-1=0. In corrispondenza delle radici di questa semplice equazione di secondo x1,2 si troveranno un punto di massimo o di minimo: R(x1, f(x1)) e S(x2, f(x2)).
Δ=36+12=48 → Δ>0
x1,2 = (6±(4√3))/6 quindi:
x1 = 1-(2√3)/3 ≅ -0.2 → f(x1) ≅ 4.1 → R(-0.2, 4.1)
x2 = 1+(2√3)/3 ≅ +2.2 → f(x2) ≅ 17.9 → S(2.2, 17.9)
Per determinare cosa siano R ed S, occorre lo studio della crescenza e decrescenza dalla derivata prima, ovvero il suo studio del segno. Si pone f'(x)>0 ed essendo una fratta si prosegue nel solito modo:
N'(x)>0 : 3x2-6x -1>0; la cui soluzione, avendo appena trovato le radici, x1,2= 1±(2√3)/3 ed essendo Δ>0 e a>0, è data dall’insieme: {∀x∈R/(x< 1-(2√3)/3 ∧ x > 1+(2√3)/3 }.
D'(x)>0 :(x-1)2>0 è un quadrato di binomio, quindi sempre positivo {∀x∈R/ x≠1} (tranne che per il valore per cui è nullo e che doveva essere escluso a priori non facendo parte del C.E.)
x1 0 x2
N'(x)>0 : + +)- – – -(+ + +
D'(x)>0 : + + + + + +O+ + +
Segno: + ) – )1( +
CRESCE⇑|⇓DECR.⇓|⇑ CRESCE
quindi: R=MAX S=MIN
Concludiamo che R(x1, f(x1)) è un massimo perchè prima la funzione cresce e poi decresce (ed esiste f(x1)); mentre S(x2, f(x2)) è un minimo.
Ricapitolando: MAX(1-(2√3)/3, ∼-0.2) e MIN(1+(2√3)/3, ∼17.9) che approssimiamo per disegnare il grafico a ∼MAX((-0.2, 4.1) e ∼MIN((+2.2, 17.9).
Ora si dovrebbe studiare la concavità e convessità della funzione, attraverso lo studio del segno della derivata seconda e si pone f”(x)>0. Tuttavia poiché la funzione non presenta particolari difficoltà interpretative, appare superfluo ai fini del disegno del grafico, tuttavia lo si svolge solo come mero esercizio. In questo caso chiamiamo per semplicità g(x) la derivata prima:
g(x)=f'(x)
g(x) = (3x2 – 6x – 1)/(x-1)2 che essendo fratta si deriva con la solita regoletta:
g'(x)=(N(x)/D(x))’ = (N'(x)D(x)-N(x)D'(x))/(D(x))2
N'(x)= (6x-6); D'(x)= (2x-2) quindi:
g'(x)= ((6x-6)(x2-2x+1)-(3x2-6x-1)(2x-2))/(x-1)4=
=[6(x-1)(x-1)2 – 2(3x2-6x-1)(x-1)]/(x-1)4=
=2(x-1)[(3(x-1)2 -(3x2-6x-1)]/(x-1)4=
=2(x-1)[(3x2+3-6x-3x2+6x+1)]/(x-1)4=
=8(x-1)/(x-1)4
quindi:
f”(x)=8(x-1)/(x-1)4
ovvero:
(x-1)/(x-1)4 >0
Al solito si studiano separatamente N”(x)>0 e D”(x)>0 e controlliamo i segni:
N”(x)>0 → (x-1)>0 →x>1
D”(x)>0 → (x-1)4>0 {∀x∈R/x ≠1}
0 x=1
N”(x)>0 : – – – – -(+ + + +
D”(x)>0 : + + + + +O+ + + +
Segno: – )1( +
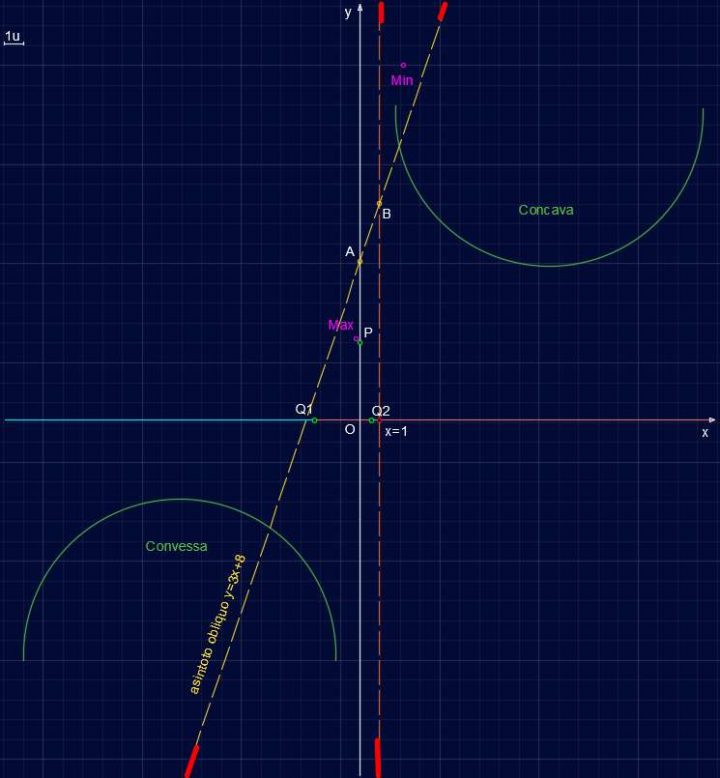
CONVESSA ∩ | ∪ CONCAVA
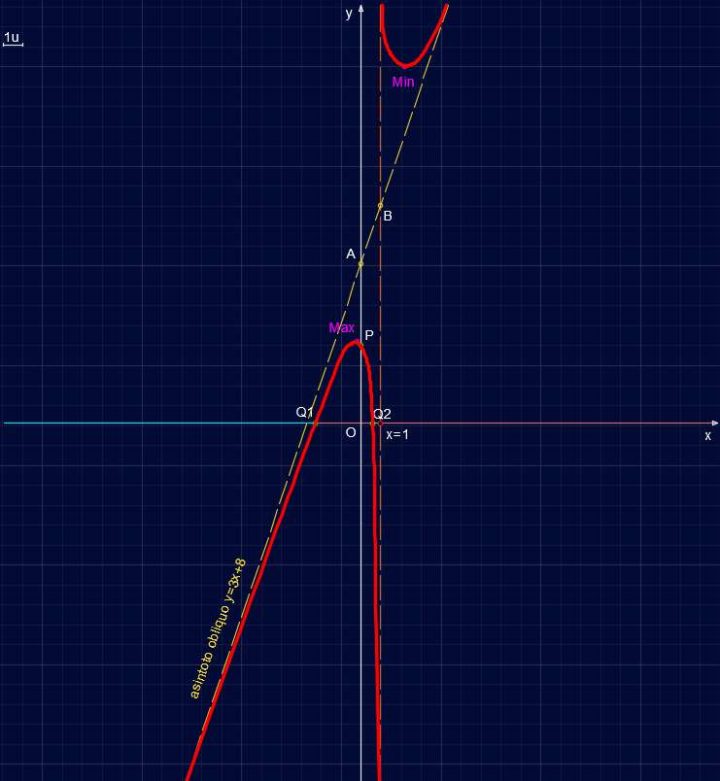
Possiamo finalmente passare a disegnare il grafico della funzione completo.
E questo è quanto.
Link utili:
- Campo di esistenza (parte 1 e parte 2)
- Discontinuità di una funzione
- Asintoti verticali, Asintoti orizzontali, Asintoti obliqui
- Analisi matematica (wikipedia)