Campo di esistenza di funzioni matematiche – II
Il campo di esistenza delle funzioni matematiche. Definizioni e applicazione alle funzioni più comuni. Seconda parte
Il campo di esistenza di una funzione si definisce come l’insieme dei valori che si possono attribuire alla variabile x per ottenere il valore della y.
Funzione esponenziale:
![]()
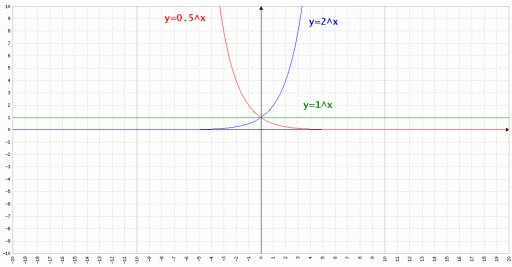
Il coefficiente a deve essere positivo strettamente in quanto la potenza risulta definita solo se la base è positiva. Se infatti si considera a = -3, dando ad x il valore ½, si ottiene y(½) = √(-2) che nel campo reale non ha senso. Per questa funzione si possono distinguere tre casi:
- 0<a<1 : funzione esponenziale decrescente;
- a=1: diventa una funzione costante;
- a>1: funzione esponenziale crescente.
Il campo di esistenza della funzione, sotto queste ipotesi, è tutto R in tutti e tre casi; ovviamente per a = 1 non si parla più di funzione esponenziale.
![]()
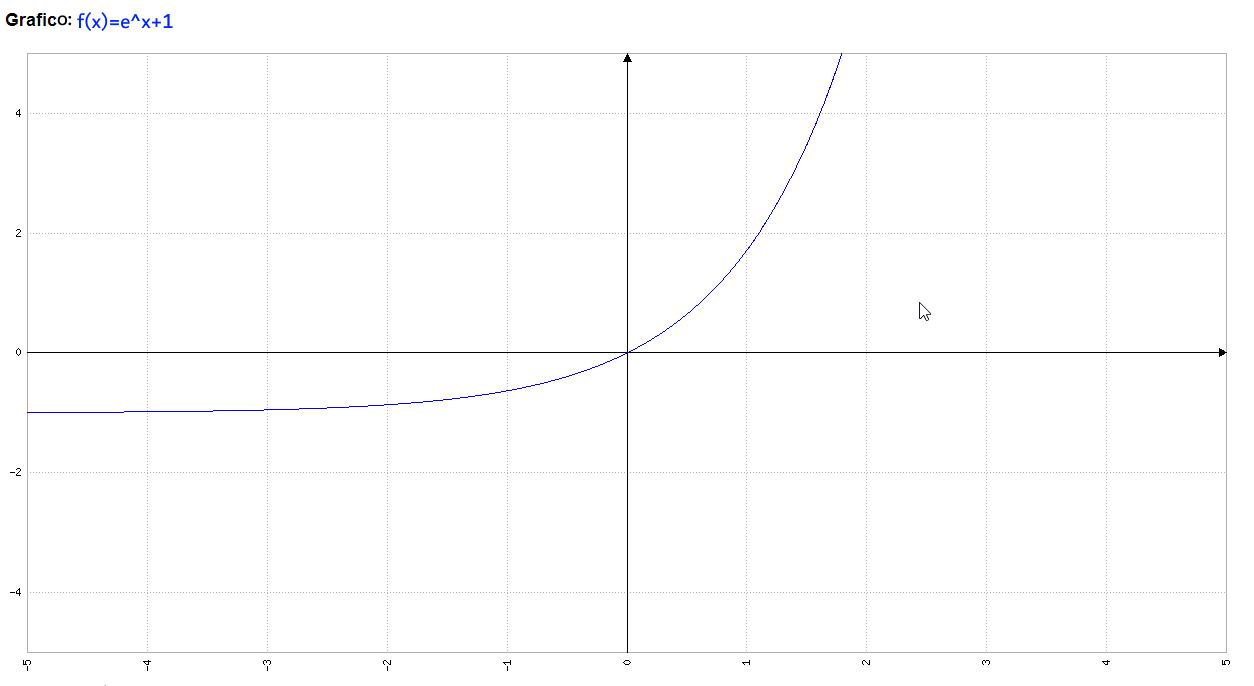
Notare che la funzione assume solo valori positivi strettamente.
Esempio:
Funzione logaritmica:
![]()
Il coefficiente a detto base del logaritmo, deve essere positivo strettamente in quanto il logaritmo è la funzione inversa della funzione esponenziale. Infatti la potenza risulta definita solo se la base è positiva. Se si considera a = -3, dando ad x il valore ½, si ottiene y(½) = √(-2) che nel campo reale non ha senso, per cui, non potendo essere usati come base per le potenze i numeri negativi essi non sono utilizzabili nemmeno come basi dei logaritmi. Ad esempio, risolvere il logaritmo:
![]()
significa risolvere l’equazione a secondo membro, che nel campo reale non ha senso.
Per questa funzione si possono distinguere due casi:
- 0<a<1 : funzione logaritmica decrescente;
- a>1: funzione logaritmica crescente.
Il campo di esistenza della funzione, sotto queste ipotesi, è tutto R+ in tutti e due casi.
![]()
Esempio:
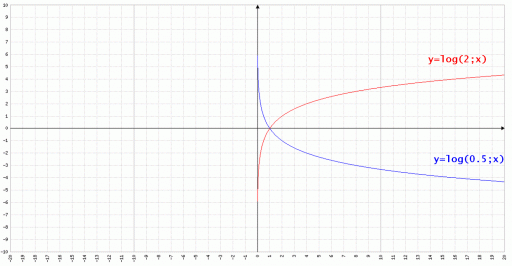
Funzione logaritmica
Funzione potenza:
![]()
La funzione potenza è definita su tre casi:
- a intero positivo;
- a intero negativo;
- a razionale.
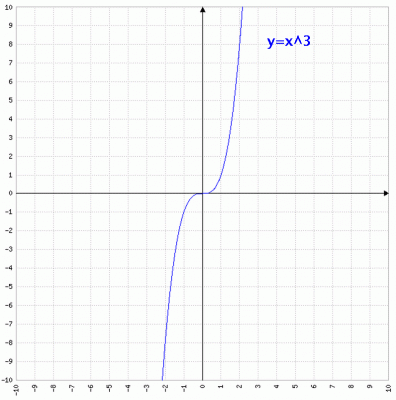
Nel primo caso, a intero positivo, la funzione è definita in tutto l’insieme dei numeri reali; perciò il campo di esistenza sarà:
![]()
Esempio 1:
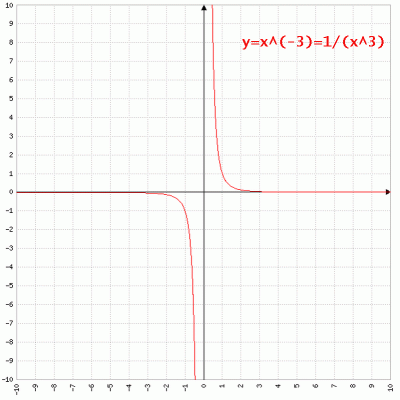
Nel secondo caso, a intero negativo, la funzione è definita in tutto l’insieme dei numeri reali tranne lo zero; perciò il campo di esistenza sarà:
![]()
Esempio 2:
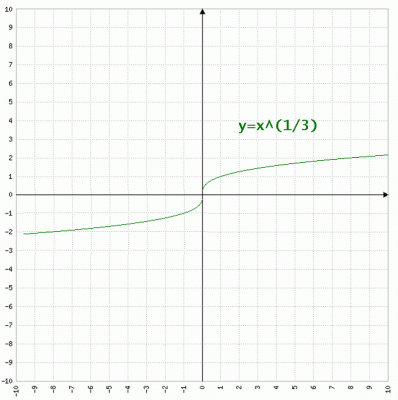
Nel terzo caso, a razionale, la funzione è definita in tutto l’insieme dei numeri reali; perciò il campo di esistenza sarà:
![]()
Esempio 3: