Asintoti orizzontali – Matematica
Gli asintoti orizzontali di una funzione matematica
In generale gli asintoti sono delle rette alle quali i punti della funzione si avvicinano indefinitamente all’infinito. Gli asintoti possono essere orizzontali, verticali od obliqui. In particolare gli asintoti orizzontali sono delle rette parallele all’asse delle ascisse. In questo articolo si studierà l’asintoto orizzontale e come fare a determinarlo. In matematica, un altro modo di di parlare di asintoti è dire che esso è una retta tale che la distanza tra essa e la funzione y = f (x) tende a 0.
Asintoto orizzontale
La retta y=k è un asintoto orizzontale per la funzione f(x) se si verifica una almeno delle seguenti condizioni:
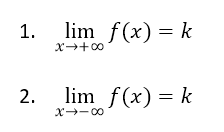Ovvero i limiti a +infinito o a -infinito devono tendere a un valore finito k. Notare che non necessariamente i due limiti devono coincidere. In pratica la funzione all’infinito tende a coincidere con la retta di equazione y=k . Grazie al calcolo del limite si riesce quindi a determinare proprio questa retta.
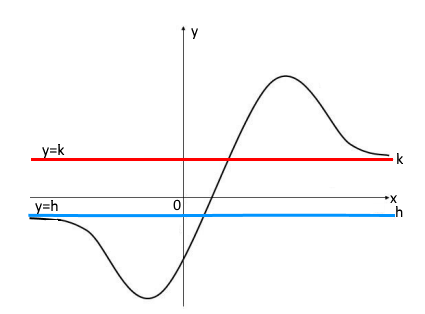
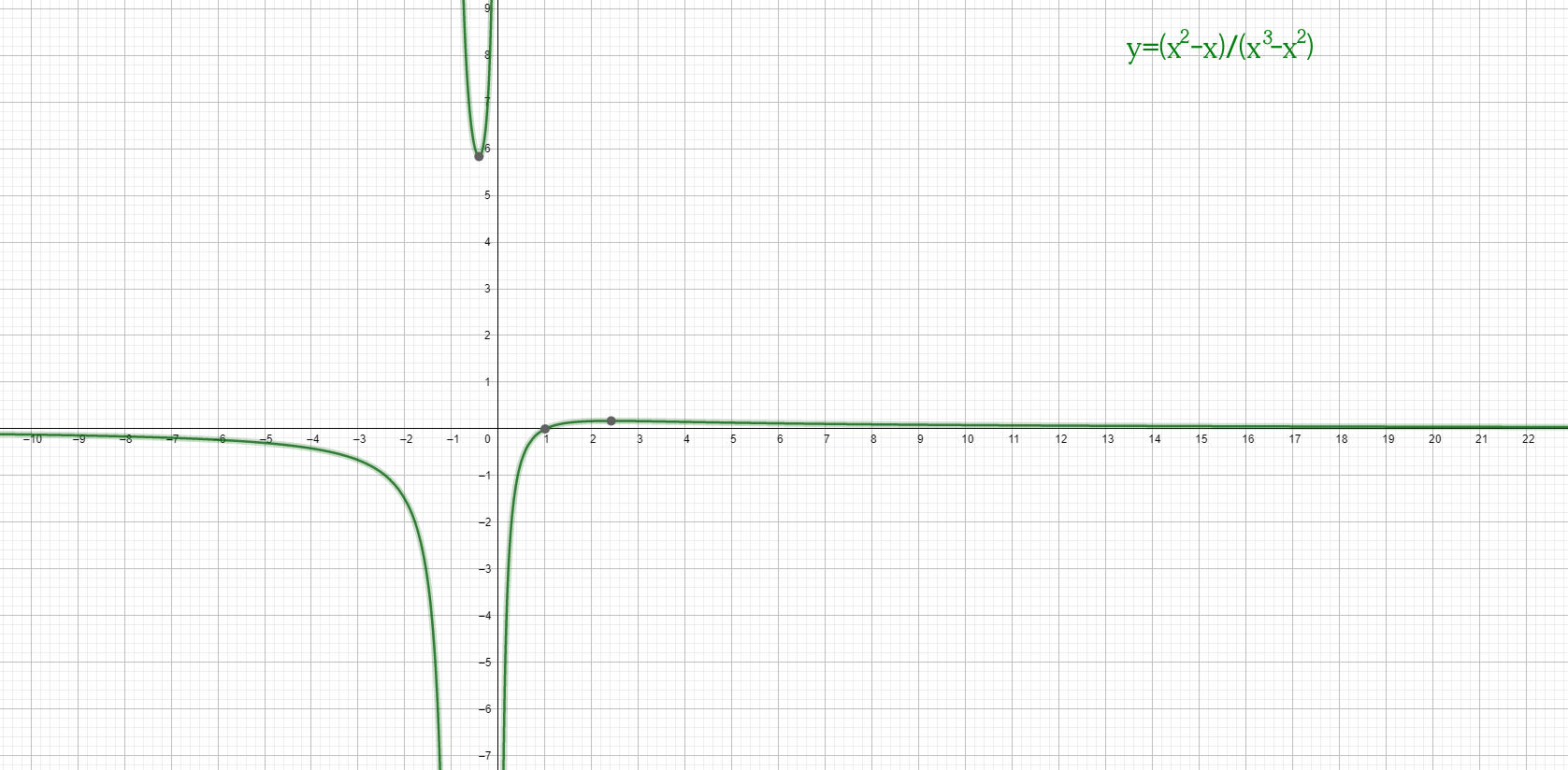
Nell’esempio sopra la funzione nel grafico presenta due asintoti orizzotali, uno destro e uno sinistro, in quanto i sui limiti a infinito sono diversi, ma finiti. In particolare se si calcola il limite per x tendente a− ∞ si ha un Asintoto Orizzontale Sinistro (A.O.S.), se si calcola il limite per x tendente a + ∞ si ha un Asintoto Orizzontale Destro (A.O.D.). Se i due asintoti coincidono, allora si parla di Asintoto Orizzontale (A.O.).
Note:
- Una funzione può ammettere al massimo due tra orizzontali e obliqui, se uno è orizzontale e l ‘altro è obliquo, devono stare in parti opposte (+infinito e -infinito e viceversa).
- Se il campo di esistenza è un intervallo limitato, non è necessario cercare nè asintoti orizzontali nè obliqui.
- Se la funzione è razionale intera non ci sono asintoti di nessun tipo.
- Se non esiste l’asintoto orizzontale non è detto che esista quello obliquo.
