Circonferenza P072 – Problemi di Geometria Euclidea
Circonferenza P072 – Problemi risolti di Geometria Euclidea
Una serie di problemi di geometria euclidea risolti durante le ripetizioni date a studenti di Liceo Scientifico, presi da vari testi scolastici. Circonferenza P072 è un problema di difficoltà medio-alta (se non altro per la sua lunghezza), preso dal testo edito da Zanichelli, che sembra essere la continuazione del P071. Il procedimento risolutivo in effetti è identico.
Traccia del problema sulla Circonferenza P072
In una circonferenza di centro C le corde AB e PQ sono congruenti e si intersecano in O, interno alla circonferenza. Dimostra che CO è la bisettrice dell’angolo formato dalle due corde. (fonte: Zanichelli – Matematica)
Ipotesi:
- AB ≅ PQ
- O punto di intersezione interno, che forma i segmenti: AO, OB e PO, OP.
Tesi:
AOC ≅ COQ;
Dimostrazione:
Fase 1-2: Disegniamo la circonferenza di centro C e le corde AB e PQ. Segniamo anche il punto di intersezione O. A questo punto uniamo gli estremi delle corde con il centro C, ottenendo i triangoli isosceli ABC e PQC. Notare che AC,BC,PC,PQ sono tutti raggi della circonferenza. Segniamo anche le intersezioni D ed E. I triangoli ottenuti sono tra loro congruenti, per il terzo criterio di congruenza dei triangoli in quanto:
- AC≅PC in quanto raggi della stessa circonferenza
- BC≅CQ in quanto raggi della stessa circonferenza
- AB≅PQ per ipotesi
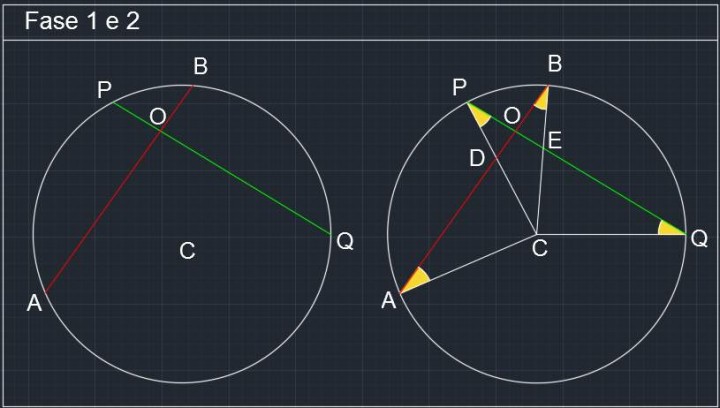
Circonferenza P072 -01- Problemi di Geometria Euclidea
Fase 3: Questo ci permette di dire che anche gli angoli sono tra loro congruenti, in particolare gli angoli ACB ≅ PCQ. Notare che alla stessa conclusione si arriva dicendo che gli angoli al vertice di corde congruenti di una stessa circonferenza sono congruenti. Quindi i seguenti angoli sono: A≅B≅P≅Q.
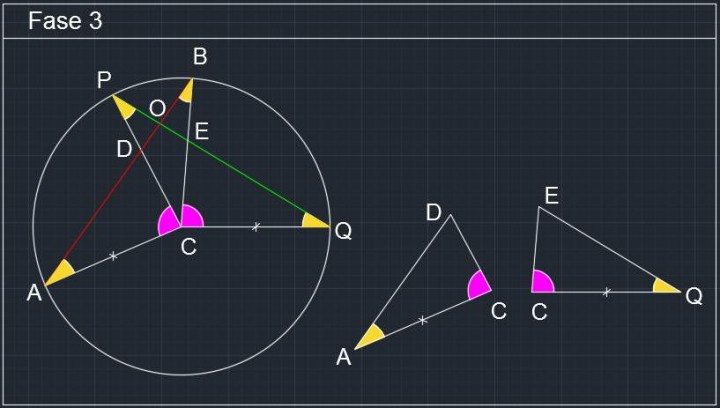
Circonferenza P072 -02- Problemi di Geometria Euclidea
A questo punto, considerando gli angoli ACP e BCQ questi sono tra loro congruenti in quanto, preso l’angolo PCB si ha:
- ACP ≅ ACB – PCB e anche:
- BCQ ≅ PCQ – PCB , da cui sottraendo membro a membro si ottiene:
- ACP – BCQ ≅ (ACB-PCQ) -PCB+PCB, ovvero:
- ACP – BCQ ≅ 0 e quindi
- ACP ≅ BCQ
Considerando i triangoli ACD e ECQ possiamo affermare che sono tra loro congruenti per il secondo criterio di congruenza, in quanto:
- AC ≅ CQ in quanto raggi della stessa circonferenza
- L’angolo in A ≅ Q come dimostrato sopra.
- L’angolo ACP ≅ BCQ come appena dimostrato.
Fase 4-5: Dalla congruenza dei triangoli ACD e ECQ possiamo affermare la congruenza degli angoli ADC ≅ CEQ. Notiamo poi che ADC ≅ PDB e CEQ ≅ PEB in quanto angoli opposti al vertice (rispettivamente vertice D ed E). Quindi sono tutti congruenti: ADC ≅ PDB ≅ CEQ ≅ PEB. Infine gli angoli POA e BOQ sono a loro volta congruenti in quanto opposti al vertice O : POA ≅ BOQ. Considerando poi i lati DC e EC si ha: DC≅EC.
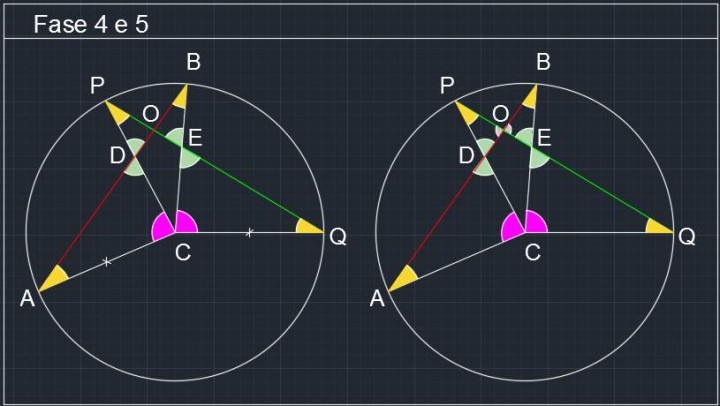
Circonferenza P072 -03- Problemi di Geometria Euclidea
Fase 6: Consideriamo ora i segmenti PD e BE; possiamo scrivere senz’altro che:
- PD ≅ PC – DC
- BE ≅ BC – EC, sottraendo menbro a membro:
- PD – BE ≅ (PC – BC) – DC + EC
- PD – BE ≅ 0
- PD ≅ BE
Questo ci permette di applicare ai triangoli POD e BOE il secondo criterio di congruenza:
- PD ≅ BE, come appena dimostrato;
- PDB ≅ PEB come dimostrato in precedenza;
- P ≅ B come dimostrato in precedenza.
In particolare sono congruenti i lati DO e OE.
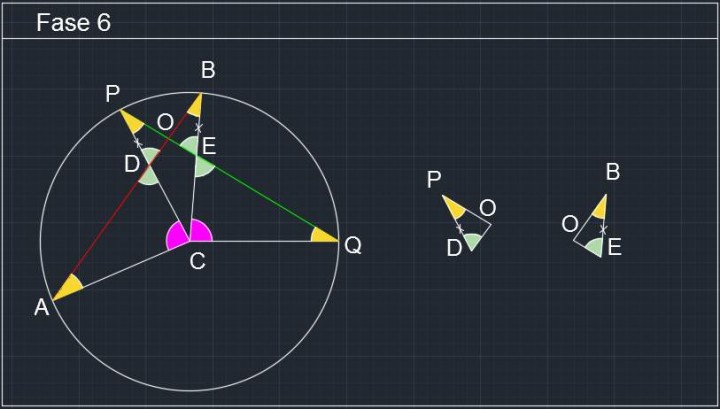
Circonferenza P072 -04- Problemi di Geometria Euclidea
Fase 7-8: Considerando gli angoli BDC e PEC, questi sono congruenti in quanto complementari di angoli uguali:
- CDB ≅ ADB – ADC
- PEC ≅ PEQ – CEQ;
Notare che ADC ≅ CEQ per la congruenza dei triangoli ADC e CEQ.
Considerando adesso i triangoli ODC e OCE, questi sono congruenti per il primo criterio di congruenza:
- DO ≅ OE come appena dimostrato;
- DC ≅ CE come dimostrato in precedenza;
- CDB ≅ PEC
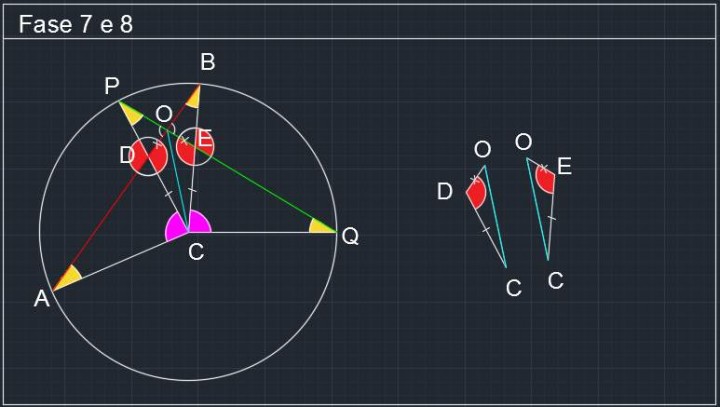
Circonferenza P072 -05- Problemi di Geometria Euclidea
Saranno perciò congruenti tutti gli angoli e in particolare, AOC ≅ COQ:
C.V.D.
Nota: ovviamente questo può essere considerato solo uno dei tanti possibili procedimenti per raggiungere la soluzione.