Analisi Matematica – Paniere Ecampus – AM015-02
Analisi Matematica – Paniere Ecampus – AM015-02
Una serie di problemi e quesiti di Analisi Matematica risolti durante le ripetizioni date a studenti del primo anno di università di varie facoltà di Ingegneria, presi dal paniere Ecampus – Ingegneria Industriale. Analisi Matematica – AM015-02 è un quesito di difficoltà medio-bassa.
Traccia del problema di Analisi Matematica – AM015-02
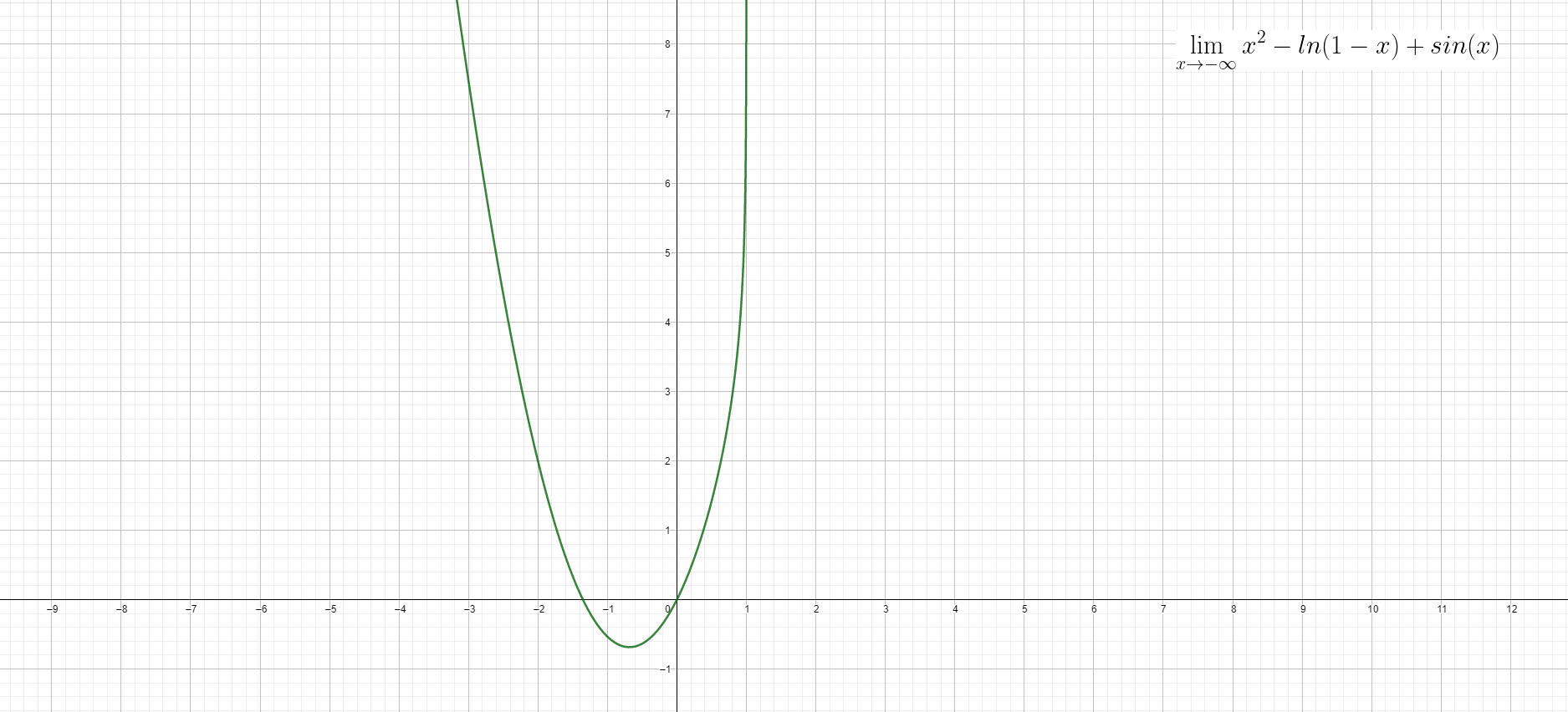
Il limite per x che tende a -∞ di x2-ln(1-x)+sin(x):
1) non esiste;
2) vale 0;
3) vale -3;
4) vale +∞.
Soluzione
Analisi Matematica – f(x)=x^2-ln(1-x)+sin(x) – Grafico della funzione – AM015-02
Questo limite è abbastanza semplice da risolvere. Conviene ricordarci la regola del confronto tra infiniti, in questo caso, si tratta di funzioni diverse. All’infinito f(x)=x cresce piu velocemente di un una f(x)=ln(x), a maggior ragione una f(x)=x2. Per quanto riguarda il f(x) = sin(x), all infinito assume comunque un valore finito, anche se non noto, compreso tra [-1, +1]. Pertanto:
\(\lim_{x\rightarrow -\infty}x^2-ln(1-x)+sin(x) = \) \(= \lim_{x\rightarrow -\infty}(-\infty)^2-ln(\infty)+sin(\infty) = \) \( =+\infty+n\epsilon [-1,+1]=+\infty \)
E questo è quanto, salvo errori od omissioni.
Link utili:
- Limite di funzione (Wikipedia)
- UniEcampus (Sito ufficiale)
Elenco AM Ecampus
[el5f806349973d5]
