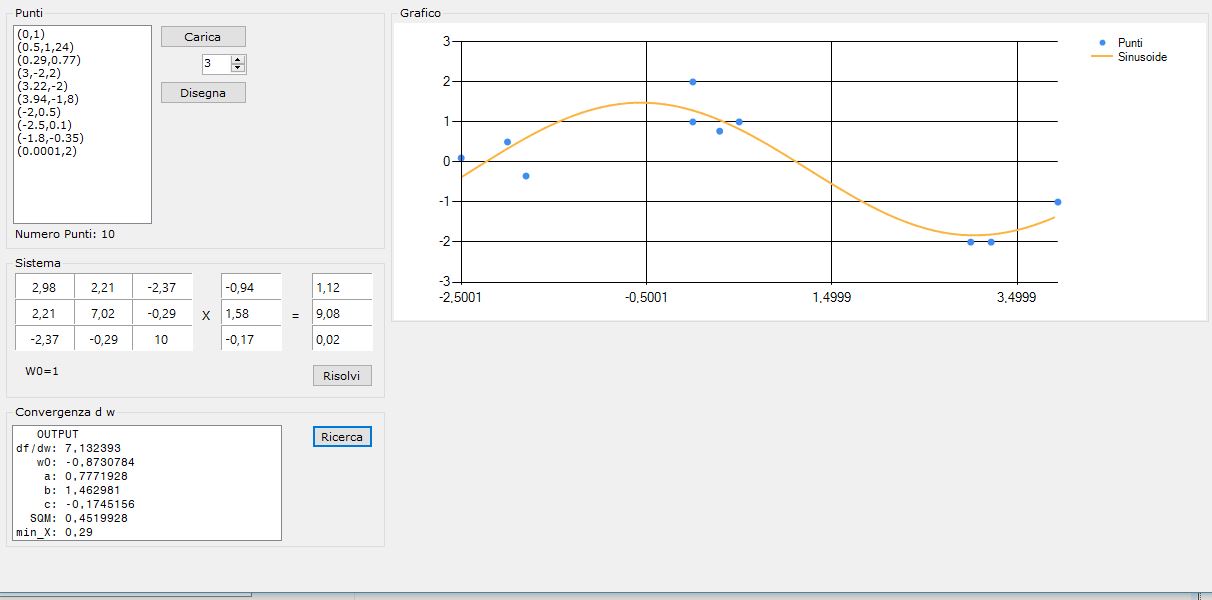
Regressione Sinusoidale e Visual Basic – Parte 1
Regressione Sinusoidale: un breve riepilogo e implementazione in Visual Basic. NET – (PARTE 1: premesse matematiche).
La regressione dei dati consiste nel trovare una funzione che approssimi tali dati col minore errore possibile. Un esempio classico è quello detto dei “Minimi Quadrati“, che rappresenta una regressione lineare, in quanto vengono stimati i parametri di una retta detta interpolante. Se, ad esempio, dei punti su un piano cartesiano si dispongono lungo una direzione predominante rettilinea, l’interpolazione lineare potrebbe essere quella più calzante. Tuttavia potremmo trovare che i dati si dispongano, a occhio, in maniera somigliante a una sinusoide o presentare degli “assembramenti” periodici: in tal caso potrebbe essere più utile usare una regressione trigonometrica o sinusoidale.
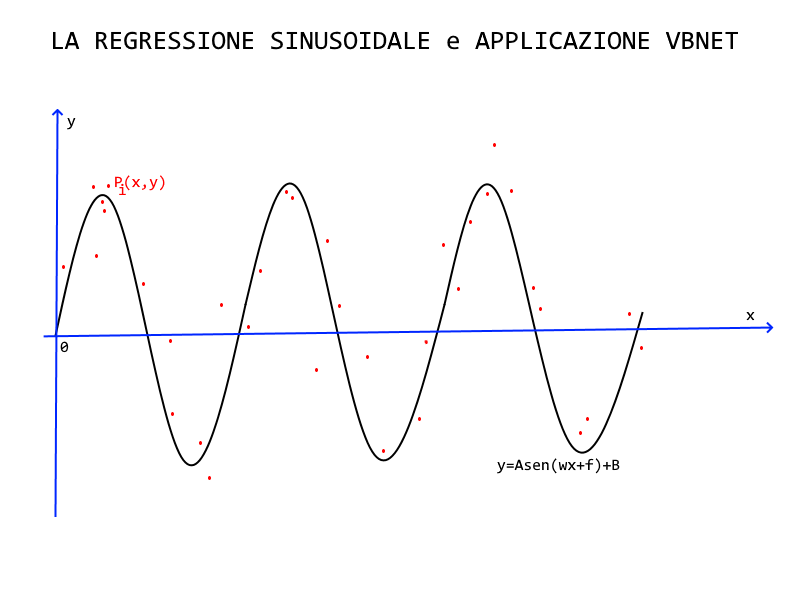
Regressione sinuosidale
Premesse matematiche
Il problema in pratica è questo: dato un insieme di n punti S={ (x1,y1); (x2,y2);…(xn,yn) } si vuole trovare una funzione del tipo y = A cos (wx+ f) + B tale che passi tra i punti suddetti, alla distanza minima possibile da essi. Per fare ciò utilizziamo il procedimento usato per i “Minimi Quadrati”. Partiamo dalla generica sinusoide:
y = A cos (wx+ f) + B
dove:
A = ampiezza d’onda (in pratica quanto è “alta”);
B = permette di traslare la sinusoide rispetto all’asse x;
w= è la pulsazione (o velocità angolare);
f = è la fase (posizione iniziale delle creste);
x = ascissa.
Applico e formule di addizione-sottrazione:
cos(wx+ f) = sen(wx)cos(f) + cos(wx)sen(f)
ottengo:
y = A sen(wx)cos(f) + A cos(wx)sen(f) + B
per semplicità pongo:
A cos(f) = a
A sen(f) = b
B = c
quindi ottengo:
y=a sen(wx) + b cos(wx) + c
La funzione del quadrato degli scarti è:
F= ∑(yk – yk)2
dove:
yk è l’ordinata della funzione interpolante;
yk è l’ordinata dei punti dati;
(la sommatoria è su k =1,2…n)
nel nostro caso:
F(a,b,c,w) = ∑[( a sen(wx) + b cos(wx) + c) – yk]2
(la sommatoria è su k =1,2…n)
Notare che ad esso è strettamente collegato lo Scarto Quadratico Medio:
σ = (1/√n) √{∑[( a sen(wx) + b cos(wx) + c) – yk]2 }
(la sommatoria è su k =1,2…n)
Bisogna ora minimizzare questa funzione F(a,b,c,w) di quattro variabili e lo si fa derivando parzialmente nelle rispettive variabili. Si impone quindi che le derivate parziali siano nulle:
∂F/∂a = ∂F/∂b = ∂F/∂c = ∂F/∂w = 0
Svolgendo i vari passaggi (che potete trovare nel pdf appunti_regressione-sinus_p3-19 su cui mi sono parzialmente basato per la stesura di questo articolo) alla fine si ottiene un sistema NON lineare di quattro equazioni, che può essere risolto iterativamente. Le prime tre equazioni permettono di ricavare a0, b0, c0 se si fissa un valore per w = w0. Si passa successivamente a calcolare:
∂F/∂w = 0
Si procede assegnando vari valori di w fino a trovare il w* di convergenza. Trovato questo valore si procede iterativamente fino a trovare due valori w*1 e w*2 per cui
F'(a1, b1, c1,w*1)*F'(a2,b2,c2,w*2) < 0
ovvero riducendo accettabilmente l’intervallo [w*1; w*2]. Notare che alla fine si è ritenuto di calcolare che la differenza di scarto quadratico medio tra due successive iterazioni fosse minore di una certa quantità piccola a discrezione: |σ( w*1) – σ( w*2)|< ε
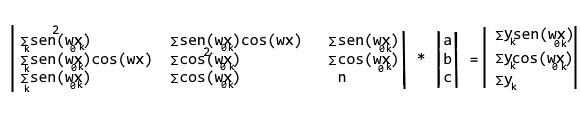
Sistema finale Regressione trigonometrica
Nella seconda parte implementeremo la risoluzione in VB.NET di questo sistema. Nel frattempo se vuoi approfondire la questione, eccoti alcuni link utili:
- Regressioni ed equazioni integrali (in francese);
- I sistemi lineari (Wikipedia);
- I sistemi non lineari (Wikipedia);
- Vai alla parte 2 o alla parte 3 o alla parte 4 o vai alla parte 5.
- Eseguibile e alcune serie di punti qui: Regressione Sinusoidale