Regressione Sinusoidale e Visual Basic – Parte 3

by Romoletto Blog · 30 Aprile 2020

Regressione Sinusoidale: un breve riepilogo e implementazione in Visual Basic. NET – (PARTE 3: Ricerca della convergenza del parametro w₀ in VB.NET).

Una volta trovati a₀, b₀, c₀ con il valore inziale di w₀ si passa a cercare la sua convergenza (o meglio: si cercherà il valore di w₀ tale per cui lo scarto quadratico medio è minimo). Prima di poter fare questo però occorre passare in visual basic la derivata:

∂F/∂w = 0 (vedi parte 1)

che esplicitata diventa:

∂F/∂w = 2 {(a²-b²)∑x_k sin(wx_k)cos(wx_k) +
+ 2ab∑x_k cos²(wx_k) – ab∑x_k +
+ a[c∑cos(wx_k) – ∑x_ky_kcos(wx_k)] +
– b[c∑sin(wx_k) -∑x_ky_ksin(wx_k)]} = 0

Romoletto Blog ti consiglia...

Nespresso Citiz EN167.B, Macchina da Caffè di De'Longhi, Sistema Capsule Nespresso, Serbatoio acqua 1L, Colore Limousine Black

In omaggio buono da 40€ spendibile sull'acquisto di prodotti nespresso. ...

Nota: prodotto fornito da Amazon

(ogni sommatoria è su k =1,2…n)

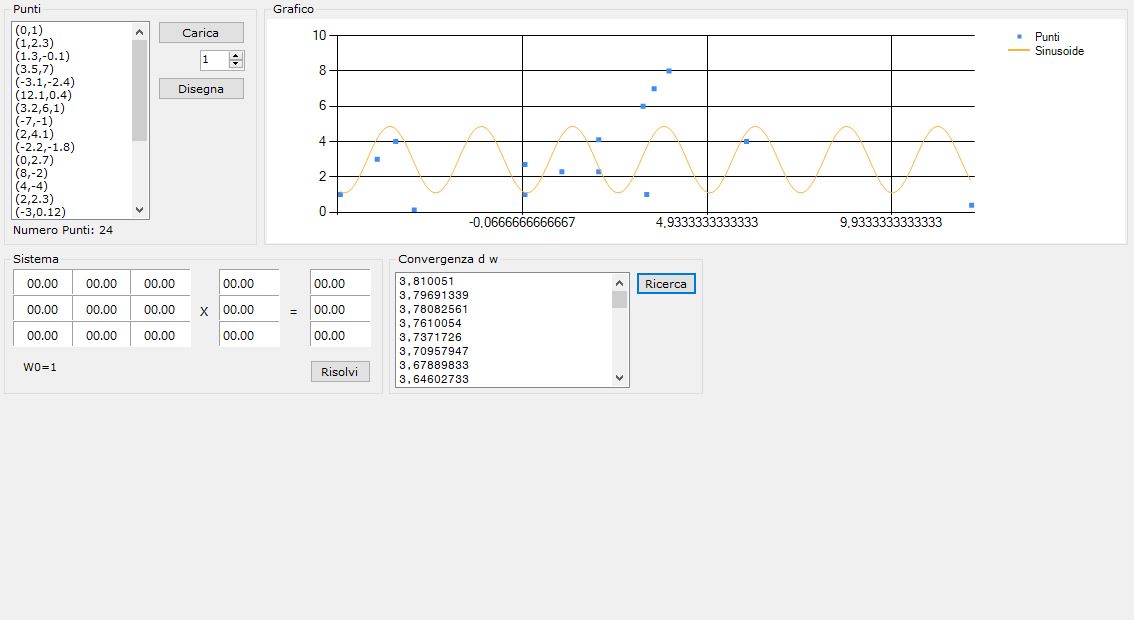
Regressione sinusoidale – Prima approssimazione – Funz 1

In questa derivata vengono sostituite le soluzioni del precedente sistema, ottenendo quindi un valore numerico. Ci prepariamo le sommatorie attraverso la funzione Calcola_Sommatorie_dFdw():

[codesyntax lang=”vbnet”]

 Function Calcola_Sommatorie_dFdw(w0 As Single) As Single()

        Dim SS(9) As Single

        For i = 0 To Numero_Punti - 1
            ' ∑xk sin(wxk)cos(wxk)
            SS(0) += Math.Sin(w0 * Vettore_Ax(i)) * Math.Cos(w0 * Vettore_Ax(i))
            ' ∑xk cos2(wxk)
            SS(1) += (Math.Cos(w0 * Vettore_Ax(i))) ^ 2
            ' ∑xk
            SS(2) += Vettore_Ax(i)
            ' ∑cos(wxk)
            SS(3) += Math.Cos(w0 * Vettore_Ax(i))
            ' ∑xkykcos(wxk)
            SS(4) += Vettore_Ax(i) * Vettore_Ay(i) * Math.Cos(w0 * Vettore_Ax(i))
            ' ∑sin(wxk)
            SS(5) += Math.Sin(w0 * Vettore_Ax(i))
            ' ∑xkyksin(wxk)
            SS(6) += Vettore_Ax(i) * Vettore_Ay(i) * Math.Sin(w0 * Vettore_Ax(i))
        Next
        Return SS

    End Function

[/codesyntax]

con la quale calcoliamo i valore numerico della derivata ∂F/∂w. (In realtà anche questo calcolo serve a ben poco: inizialmente si era pensato di trovare il valore di w0 che rendeva più vicina a zero proprio questa derivata).

[codesyntax lang=”vbnet”]

Function dFdw(a0 As Single, b0 As Single, c0 As Single, w0 As Single) As Single

        '∂F/∂w = 2 {(a2-b2)∑xk sin(wxk)cos(wxk) +
        '+ 2ab∑xk cos2(wxk) - ab∑xk +
        '+ a[c∑cos(wxk) - ∑xkykcos(wxk)] +
        '- b[c∑sin(wxk) -∑xkyksin(wxk)]} 

        Dim SS() As Single = Calcola_Sommatorie_dFdw(w0)

        dFdw = 2 * (
        (a0 ^ 2 - b0 ^ 2) * SS(0) +
        2 * a0 * b0 * SS(1) - a0 * b0 * SS(2) +
        a0 * (c0 * SS(3) - SS(4)) -
        b0 * (c0 * SS(5) - SS(6))
        )

    End Function

[/codesyntax]

A questo punto ci occorre conoscere a quale valore di w₀ dobbiamo prendere per far si che l’uguaglianza a zero della derivata sia verificata o comunque molto piccola. Ci sviluppiamo il calcolo dello Scarto Quadratico Medio con la funzione Calcola_SQM():

[codesyntax lang=”vbnet”]

    Function Calcola_SQM(a0 As Single, b0 As Single, c0 As Single, w0 As Single) As Single
        'F(a,b,c,w) = ∑[( a sen(wx) + b cos(wx) + c) - yk]2

        Dim s As Single = 0
        For i = 0 To Numero_Punti - 1
            s += (((a0 * Math.Sin(w0 * Vettore_Ax(i)) + b0 * Math.Cos(w0 * Vettore_Ax(i)) + c0 - Vettore_Ay(i))) ^ 2)
        Next

        s = (s / Numero_Punti) ^ 0.5

        Return s

    End Function

[/codesyntax]

Più piccolo è lo SQM maggiore sarà la corrispondenza della sinusoide ai punti. Ora è possibile procedere su un intervallo di valori [-π,+π] fino a trovare il valore che si avvicina di più zero. Trovato questo valore si procederà alla ulteriore scansione nell’intorno di tale valore. La funzione è la dFdw_Min_VAss() che restituisce un vettore con i minimi legati allo SQM: dF/dw₀, w0, a, b, c, sqm.

[codesyntax lang=”vbnet”]

 Function dFdw_Err_Min() As Single()
        

        Dim TabMinimi(5) As Single

        TabMinimi(0) = 10 ^ 20
        TabMinimi(1) = 10 ^ 20
        TabMinimi(2) = 10 ^ 20
        TabMinimi(3) = 10 ^ 20
        TabMinimi(4) = 10 ^ 20
        TabMinimi(5) = 10 ^ 20

        For w0 = -Math.PI To Math.PI Step 0.01

            Dim sol() = Risolvi_Sistema_Lineare(w0)
            If sol IsNot Nothing Then
                Dim df = dFdw(sol(0), sol(1), sol(2), w0)
                Dim SqM = Calcola_SQM(sol(0), sol(1), sol(2), w0)
                'trova l'errore standard minimo
                If SqM < TabMinimi(5) Then
                    TabMinimi(0) = df
                    TabMinimi(1) = w0
                    TabMinimi(2) = sol(0)
                    TabMinimi(3) = sol(1)
                    TabMinimi(4) = sol(2)
                    TabMinimi(5) = SqM
                End If

            End If
        Next
        Return TabMinimi
    End Function

[/codesyntax]

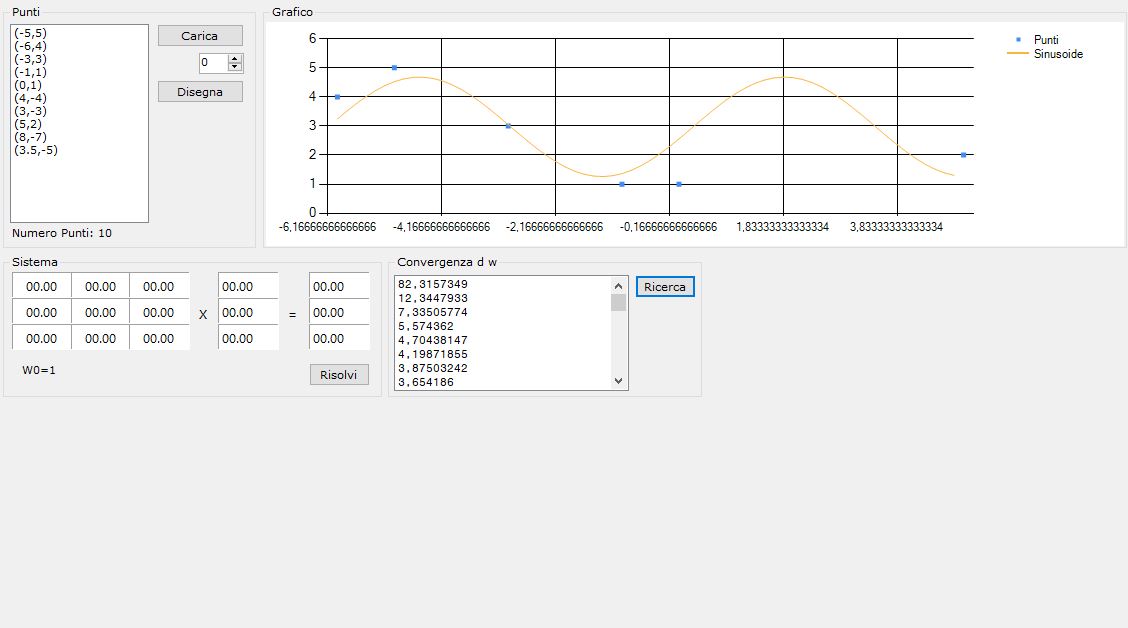
Regressione sinusoidale – Prima approssimazione – Funz 2

Nella terza parte implementeremo in VB.NET l’affinamento della soluzione trovata. Nel frattempo se vuoi approfondire la questione, eccoti alcuni link utili: