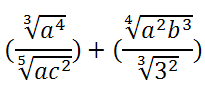Previsioni del lotto e lottologia
Interpretazione dei Sogni
Significato dei Nomi
Musica degli Spot
Ricette Semplici
Elenco Lavora con Noi
Matematica e Geometria
Fisica e Chimica
Ingegneria e Urbanistica
Hardware e Software
Listati Visual Basic .NET
Applicazioni Simple APPs
Schemi di Elettronica
Cerca su Romoletto Blog
Contatta Romoletto Blog
Regressione Sinusoidale: un breve riepilogo e implementazione in Visual Basic. NET – (PARTE 2: implementazione del sistema lineare e sua risoluzione in VB.NET).
Viste le basi teorico-matematiche del problema sulla regressione trigonometrica, passiamo ora alla sua implementazione in linguaggio basic (in ambiente VB.NET). Forse si sarebbe potuto usare un altro linguaggio come il c++ o fortran, ma essendo il vb tra quelli più facili, usato anche in Excell (vba) e alla portata di tutti, si è preferita questa opzione.
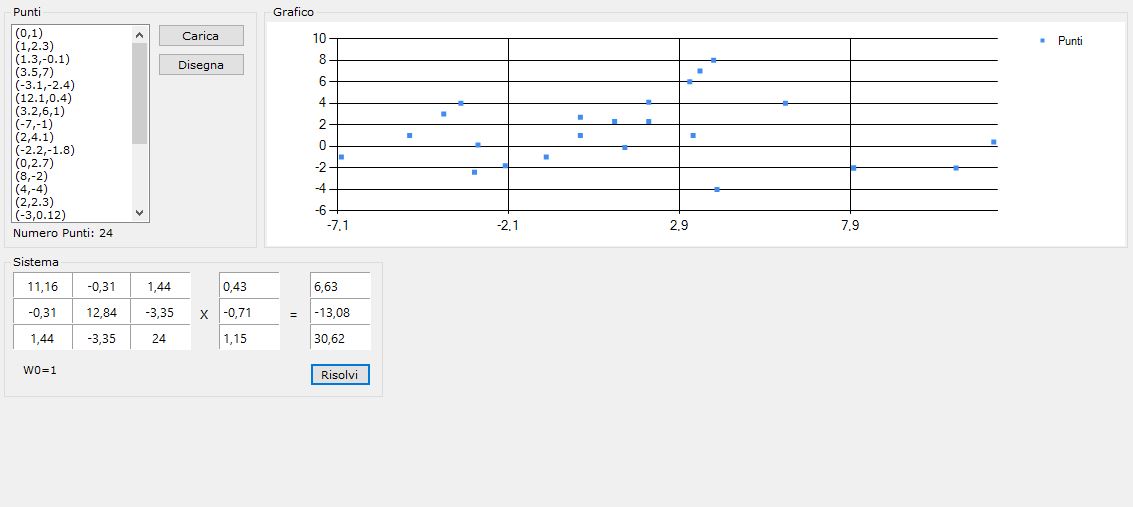
Regressione sinuosidale – dati e grafico e sistema lineare
Implementazione del sistema lineare
La prima cosa da fare è trasformare le premesse matematiche della parte 1 di questo articolo in funzioni o subroutine in vbnet. Implementiamo preliminarmente delle funzioni che ci permettano di effettuare vari calcoli matriciali per la risoluzione del sistema lineare. Il w0 di default per adesso è impostato a 1. I punti, in base alle preferenze utente, possono essere inserite a livello di programmazione oppure in un file di testo esterno.
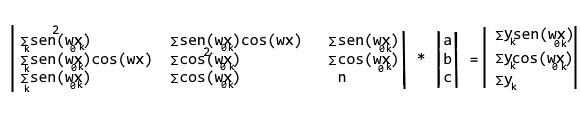
Sistema Lineare della Regressione Sinusoidale
Dichiariamo i vettori contenenti le coordinate dei punti e le variabili pubblici:
Public Vettore_Ax(10000) As Single ' contiene le ascisse dei punti
Public Vettore_Ay(10000) As Single ' contiene le ordinate dei punti
Public Numero_Punti As Integer = 0 ' numero di puntiI vettori sono ampiamente dimensionati, ma Redim Preserve può ridimensionarli a ribasso per evitare sprechi. Più punti si devono analizzare più lenta sarà l’elaborazione.
Le funzioni di base per la risoluzione del sistema
La funzione Determinante() permette di calcolare appunto di il determinante di matrici 3×3 col metodo di Sarrus:
Private Function Determinante(Matrice(,) As Single)
'solo 3x3
Dim S1 = Matrice(0, 0) * Matrice(1, 1) * Matrice(2, 2)
Dim S2 = Matrice(0, 1) * Matrice(1, 2) * Matrice(2, 0)
Dim S3 = Matrice(0, 2) * Matrice(1, 0) * Matrice(2, 1)
Dim D1 = Matrice(0, 2) * Matrice(1, 1) * Matrice(2, 0)
Dim D2 = Matrice(0, 0) * Matrice(1, 2) * Matrice(2, 1)
Dim D3 = Matrice(0, 1) * Matrice(1, 0) * Matrice(2, 2)
Return S1 + S2 + S3 - D1 - D2 - D3
End FunctionPassiamo poi alla funzione Rango() che permette di calcolare il rango delle matrici 3×3 (ci servirà per sapere se il sistema ammette soluzioni):
Private Function Rango(Matrice(,) As Single)
'solo 3x3
Rango = 1
If Determinante(Matrice) <> 0 Then
Return 3
Else
Dim S1 = Matrice(0, 0) * Matrice(1, 1)
Dim S2 = Matrice(0, 1) * Matrice(1, 2)
Dim D1 = Matrice(0, 2) * Matrice(1, 1)
Dim D2 = Matrice(0, 0) * Matrice(1, 2)
If S1 + S2 - D1 - D2 <> 0 Then Return 2
End If
End Function(Nota: in realtà poi questa funzione non si è mai usata, ma può sempre essere utile per altri scopi). Implementiamo ora il sistema, o meglio le sue matrici. Calcoliamo la matrice dei coefficienti tramite la funzione Calcolo_Matrice_Coefficienti_x_Punto() per ogni singolo punto; i valori trovati saranno passati poi alla funzione successiva che effettua le sommatorie. Nulla impedisce di inglobare le due funzioni in una sola.
Private Function Calcolo_Matrice_Coefficienti_x_Punto(CX As Single, CY As Single, Optional w0 As Single = 1)
'input coordinate dei punti
'output matrice 3x3 sistema
'matrice dei coefficienti
Dim M3x3(2, 2) As Single
M3x3(0, 0) = (Math.Sin(w0 * CX)) ^ 2
M3x3(0, 1) = (Math.Sin(w0 * CX)) * (Math.Cos(w0 * CX))
M3x3(0, 2) = (Math.Sin(w0 * CX))
M3x3(1, 0) = (Math.Cos(w0 * CX)) * (Math.Sin(w0 * CX))
M3x3(1, 1) = (Math.Cos(w0 * CX)) ^ 2
M3x3(1, 2) = (Math.Cos(w0 * CX))
M3x3(2, 0) = (Math.Sin(w0 * CX))
M3x3(2, 1) = (Math.Cos(w0 * CX))
M3x3(2, 2) = 1
Return M3x3
End FunctionStesso procedimento con la matrice delle soluzioni tramite Calcolo_Matrice_Termini_Noti_x_Punto() i cui risultati passano alla funzione
Private Function Calcolo_Matrice_Termini_Noti_x_Punto(CX As Single, CY As Single, Optional w0 As Single = 1)
'input coordinate dei punti
'output matrice 3x3 sistema
'matrice dei coefficienti
Dim M3x1(2) As Single
M3x1(0) = CY * (Math.Sin(w0 * CX))
M3x1(1) = CY * (Math.Cos(w0 * CX))
M3x1(2) = CY
Return M3x1
End FunctionOra passiamo alla creazione della Matrice incompleta (che è costituita da sommatorie) tramite la funzione Matrice_Incompleta_Sommatoria():
Private Function Matrice_Incompleta_Sommatoria(CX() As Single, CY() As Single, Optional w0 As Single = 1)
'sommatoria
Dim Somma(2, 2) As Single
For K = 0 To Numero_Punti - 1
Dim Result = Calcolo_Matrice_Coefficienti_x_Punto(CX(K), CY(K))
Somma(0, 0) += Result(0, 0)
Somma(0, 1) += Result(0, 1)
Somma(0, 2) += Result(0, 2)
Somma(1, 0) += Result(1, 0)
Somma(1, 1) += Result(1, 1)
Somma(1, 2) += Result(1, 2)
Somma(2, 0) += Result(2, 0)
Somma(2, 1) += Result(2, 1)
Somma(2, 2) += Result(2, 2)
Next
Return Somma
End FunctionAllo stesso modo implementiamo il vettore dei termini noti (che è costituito da sommatorie) tramite la funzione Matrice_Termini_Noti_Sommatoria():
Private Function Matrice_Termini_Noti_Sommatoria(CX() As Single, CY() As Single, Optional w0 As Single = 1)
'sommatoria
Dim Somma(2) As Single
For K = 0 To Numero_Punti - 1
Dim Result = Calcolo_Matrice_Termini_Noti_x_Punto(CX(K), CY(K))
Somma(0) += Result(0)
Somma(1) += Result(1)
Somma(2) += Result(2)
Next
Return Somma
End FunctionSoluzione del sistema lineare
Adesso che abbiamo impostato le matrici del sistema [A] [X] = [B] passiamo alla sua risoluzione, con semplice metodo di Cramer per i sistemi a 3 equazioni e 3 incognite, tramite la funzione : Solve_Sistema().
Private Function Solve_Sistema(Matrice_Incompleta(,) As Single, Vettore_TN() As Single)
' usiamo il metodo di Cramer se det <>0
Dim Det = Determinante(Matrice_Incompleta)
Dim S1 As Single = 0
Dim S2 As Single = 0
Dim S3 As Single = 0
If Det <> 0 Then
'=================================
Dim A(2, 2) As Single
Dim B(2, 2) As Single
Dim C(2, 2) As Single
'=================================
A(0, 0) = Vettore_TN(0)
A(0, 1) = Matrice_Incompleta(0, 1)
A(0, 2) = Matrice_Incompleta(0, 2)
A(1, 0) = Vettore_TN(1)
A(1, 1) = Matrice_Incompleta(1, 1)
A(1, 2) = Matrice_Incompleta(1, 2)
A(2, 0) = Vettore_TN(2)
A(2, 1) = Matrice_Incompleta(2, 1)
A(2, 2) = Matrice_Incompleta(2, 2)
'=================================
B(0, 0) = Matrice_Incompleta(0, 0)
B(0, 1) = Vettore_TN(0)
B(0, 2) = Matrice_Incompleta(0, 2)
B(1, 0) = Matrice_Incompleta(1, 0)
B(1, 1) = Vettore_TN(1)
B(1, 2) = Matrice_Incompleta(1, 2)
B(2, 0) = Matrice_Incompleta(2, 0)
B(2, 1) = Vettore_TN(2)
B(2, 2) = Matrice_Incompleta(2, 2)
'=================================
C(0, 0) = Matrice_Incompleta(0, 0)
C(0, 1) = Matrice_Incompleta(0, 1)
C(0, 2) = Vettore_TN(0)
C(1, 0) = Matrice_Incompleta(1, 0)
C(1, 1) = Matrice_Incompleta(1, 1)
C(1, 2) = Vettore_TN(1)
C(2, 0) = Matrice_Incompleta(2, 0)
C(2, 1) = Matrice_Incompleta(2, 1)
C(2, 2) = Vettore_TN(2)
'=================================
Dim Det_A = Determinante(A)
Dim Det_B = Determinante(B)
Dim Det_C = Determinante(C)
S1 = Det_A / Det
S2 = Det_B / Det
S3 = Det_C / Det
Dim Soluzioni() = {S1, S2, S3}
Return Soluzioni
Else
Return Nothing
End If
End FunctionPer la risoluzione del sistema si procederà mettendo dentro un Button ad esempio la seguente funzione Risolvi_Sistema_Lineare():
Private Function Risolvi_Sistema_Lineare()
Dim W0 = 1S
Dim M_IN(,) As Single = Matrice_Incompleta_Sommatoria(Vettore_Ax, Vettore_Ay, W0)
Dim M_TN() As Single = Matrice_Termini_Noti_Sommatoria(Vettore_Ax, Vettore_Ay, W0)
Dim SOL_SL() As Single = Solve_Sistema(M_IN, M_TN)
Return SOL_SL
End FunctionLa funzione restituisce il vettore delle soluzioni. Abbiamo terminato questa seconda parte sulla regressione trigonometrica e implementazione VBnet. Nella terza parte implementeremo la ricerca del valore migliore di w0 (per ora impostato a 1), in VB.NET . Nel frattempo se vuoi approfondire la questione, eccoti alcuni link utili:
- Regola di Cramer per risolvere i sistemi lineari (wikipedia);
- Regola di Sarrus per i determinanti (wikipedia);
- Torna alla parte 1 o vai alla parte 3 o alla parte 4 o vai alla parte 5.
- Eseguibile e alcune serie di punti qui: Regressione Sinusoidale
Alcuni post della stessa categoria...
Link sponsorizzati inseriti nella pagina.
Random Post
PUBBLICITÀ
|
Disclaimer:
|
Copyright:
|
Precedente
MENU'
Successivo