Triangolo P003 – Problemi di Geometria Euclidea
Triangolo P003 – Problemi risolti di Geometria Euclidea
Una serie di problemi di geometria euclidea risolti durante le ripetizioni date a studenti di Liceo Scientifico, presi da vari testi scolastici. Triangolo P003 è un problema di difficoltà bassa, preso presumibilmente da un testo di matematica edito da Zanichelli.
Traccia del problema sul triangolo P003
Dato un triangolo isoscele di vertici ABC e base AB, si indichino con L, M, N i punti medi di ogni lato. Dimostrare che LMN è un triangolo isoscele. (fonte: presumibilmente Zanichelli – Matematica)
Ipotesi:
- L, M, N sono punti medi rispettivamente di
- AC → AL ≅ LC
- AB → AM ≅ MB
- BC → BN ≅ NC
Tesi:
- LMN è un triangolo isoscele ovvero deve avere due lati (o due angoli congruenti).
Dimostrazione:
Fase 1-2 e 3: Disegniamo il triangolo e i punti medi, in rosso segniamo il triangolo da dimostrare essere isoscele.
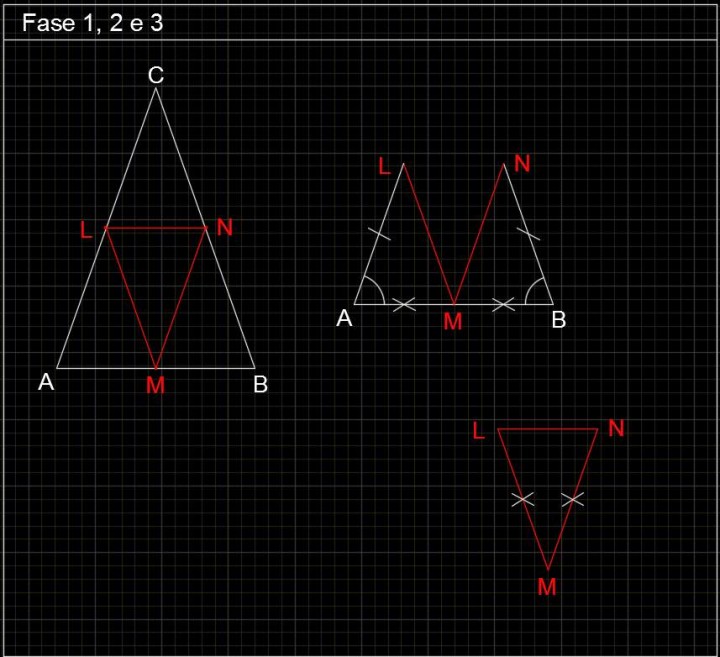
Triangolo P003 -01- Problemi di Geometria Euclidea
Partiamo quindi dalle ipotesi: il triangolo ABC è isoscele quindi:
- AC ≅ BC
- A ≅ B
I punti medi mi danno:
- AL ≅ LC
- AM ≅ MB
- BN ≅ NC
Quindi considerando i triangoli AML e MBN questi sono congruenti per il primo criterio di congruenza in quanto:
- AL ≅ BN perchè AC ≅ BC e quindi anche AC/2 ≅ BC/2;
- AM ≅ MB per ipotesi;
- A ≅ B per ipotesi
Quindi anche i lati LM e MN sono congruenti e quindi abbiamo dimostrato che LMN per avere due lati uguali è un triangolo isoscele.
C.V.D.
Nota: ovviamente questo può essere considerato solo uno dei tanti possibili procedimenti per raggiungere la soluzione. Ad essere più rigorosi, poichè i triangoli AML ed MBN sono specchiati, si sarebbe dovuti prima passare per la congruenza del triangolo ALM con LCN, poi per quella tra ALM e MBL e concludere che ALM è congruente con MNL.