Simmetrie nelle funzioni – Matematica
Lo studio delle simmetrie delle funzioni matematiche a una variabile
Studiare le eventuali simmetrie di una funzione serve a ridurre il suo studio della metà. Distinguiamo simmetrie assiali cioè rispetto ad una retta o a un asse cartesiano o simmetrie puntuali cioè rispetto ad un punto o all’origine del piano cartesiano.
Funzioni periodiche
Una funzione si dice periodica di periodo T se assume lo stesso valore in corrispondenza degli elementi del dominio che che distano T fra loro ovvero:
- f(x)=f(x+T) ∀x∈ C.E.
Esempio: y= senx
Nota: anche se non si tratta di funzioni simmetriche, è possibile comunque studiarle in un intervallo corrispondente al periodo T e ripetere il tratto di funzione infinite volte verso ±infinito.
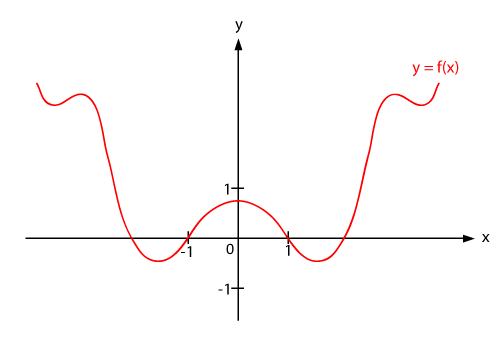
Simmetrie assiali pari
Se la funzione presenta una simmetria rispetto all’asse delle ordinate, si definisce pari e verifica la seguente proprietà:
- f(x)= f(-x) ∀x∈ C.E.
In questi casi è sufficiente studiarla nel semiasse positivo delle ascisse, per poi ribaltare il grafico nel semiasse negativo.
Simmetrie Pari
Un esempio di funzione pari è la parabola oppure la funzione biquadratica.
- y=x2
NOTA: non può esserci una simmetria rispetto all’asse delle ascisse poiché verrebbe meno la definizione stessa di funzione che è una legge che associa ad un valore della variabile x uno ed un solo valore della variabile y.
Simmetrie assiali dispari
Una funzione si dice dispari quando è simmetrica rispetto all’origine degli assi cartesiani e verifica la seguente proprietà:
- .f(x)= -f(-x) ∀x∈ C.E.
Se una funzione è dispari è sufficiente studiarla nel semiasse positivo delle ascisse, e poi ruotare il grafico di un angolo piatto nel semiasse negativo.
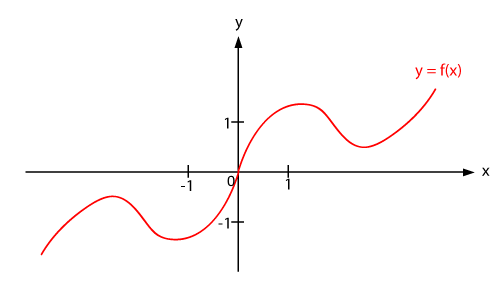
Simmetrie Dispari
Un esempio di funzione dispari è la parabola cubica o l’ iperbole equilatera.
- y=x3
Alcune proprietà delle funzioni simmetriche
- La somma di due funzioni pari è una funzione pari.
- La somma di due funzioni dispari è una funzione dispari.
- Il prodotto di una funzione pari per una costante è una funzione pari.
- Il prodotto di una funzione dispari per una costante è una funzione dispari.
- Il prodotto di due funzioni pari è una funzione pari.
- Il prodotto di due funzioni dispari è una funzione pari.
- Il prodotto di una funzione pari e di una funzione dispari è una funzione dispari.
- La derivata di una funzione pari è una funzione dispari.
- La derivata di una funzione dispari è una funzione pari.
- In generale la somma di una funzione pari e di una dispari non è né pari né dispari.
- L’unica funzione sia pari che dispari è la funzione costante f(x)=0