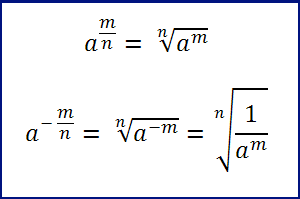I radicali aritmetici: cosa sono, come si calcolano

Definizione: la radice n-esima (n ∈ N_o, n appartenente agli interi positivi) di un numero reale positivo a è il numero b che elevato ad n dà a stesso:

\(\large \sqrt[n]{a} = b; a= b^{n} \: con: \: a\geq 0 ; b\geq 0\)

• Il numero n viene detto “indice di radice” e deve essere un numero intero strettamente positivo, n > 0;
• il simbolo √ viene chiamato “radice“;
• tutto ciò che sta dentro il simbolo di radice si chiama “radicando” o “argomento della radice” e deve essere un numero reale positivo, a ≥ 0;
• il tutto (radice, indice, radicando), sotto queste condizioni, viene chiamato “radicale aritmetico“.

Note da ricordare su radicali aritmetici

1. L’operazione con la quale si passa da a alla sua radice b si chiama “estrazione di radice“.
2. Se n = 2 la radice si chiama “radice quadrata” e non si scrive l’indice;
3. se n = 3 la radice si chiama “radice cubica“.
4. Se n = 1 allora la radice è uguale al radicando, cioè è uguale a 1.
5. La radice  n-esima di zero è zero.
6. Elevare un radicale n-esimo a n equivale a ottenere il radicando stesso come risultato:
   \(\large (\sqrt[n]{a})^{n} = a\)

Inoltre si ricordi che si usa il modulo o valore assoluto in quanto vogliamo considerare solo risultati positivi.

\(\large se\, a=b \rightarrow a^{n}=b^{n}\)

Proprietà dei radicali aritmetici

Si premette che, nelle definizioni e proprietà seguenti, n,m,p,t sono numeri interi strettamente positivi e che a,b,c sono numeri reali positivi.

Proprietà 1: la radice del radicale non cambia se radicando e indice vengono moltiplicati per lo stesso numero p ∈ N intero positivo.

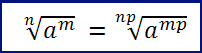
Proprietà 2: il valore di un radicale aritmetico non cambia se radicando e indice vengono divisi per un divisore comune.

 

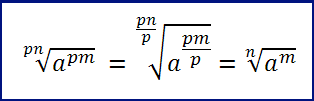
• Esempio:

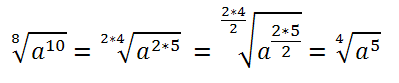
L’operazione appena vista rende “irriducibile” il radicale.

• Riduzione di più radicali allo stesso indice: è un’operazione serve a poter confrontare i radicali o applicarvi ulteriori proprietà. I radicali vanno sempre resi irriducibili. Ad esempio:

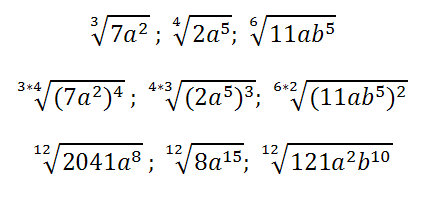
Proprietà 3 (proprietà invariantiva): moltiplicando o dividendo l’indice del radicale e l’esponente del radicando per uno stesso numero naturale, diverso da 0, il valore del radicale non varia.

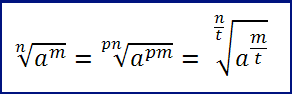
Proprietà 4: il prodotto di due radicali aventi stesso indice è un radicale dello stesso indice e con radicando uguale al prodotto dei radicandi. Vale ovviamente il viceversa.

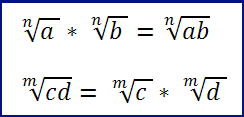
• Portare un fattore dentro radice: il fattore può essere portato sotto il segno di radice n-esima a patto di elevarlo a una potenza n-esima. Ad esempio:

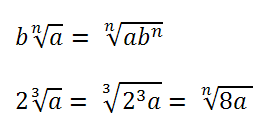
• Portare un fattore fuori radice: il fattore può essere portato fuori dal segno di radice n-esima a patto di estrarne la radice n-esima. Ad esempio:

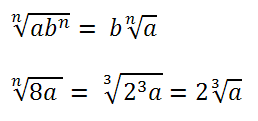
Proprietà 5: Il quoziente di due radicali aventi stesso indice è un radicale dello stesso indice e con radicando uguale al quoziente dei radicandi. Vale ovviamente il viceversa.

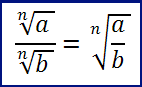
Proprietà 6: l’elevazione a potenza di un radicale equivale a elevare a quella potenza il radicando. Vale ovviamente il viceversa.

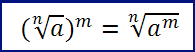
Proprietà 7: l’estrazione di radice di un radicale equivale a una radice del medesimo radicando e di indice pari al prodotto degli indici. Vale ovviamente il viceversa.

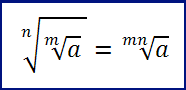
Definizione 2: le espressioni nelle quali compaiono i radicali, vengono chiamate espressioni irrazionali o espressioni radicali. Ad esempio:

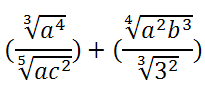
Definizione 3: razionalizzare il numeratore di una frazione significa portare il numeratore dell’espressione algebrica nella forma razionale (o intera) ovvero i radicali non compariranno più a numeratore. Ad esempio:

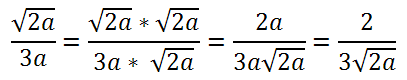
Definizione 4: razionalizzare il denominatore di una frazione significa portare l’espressione algebrica nella forma intera ovvero i radicali non compariranno più a denominatore. Ad esempio:

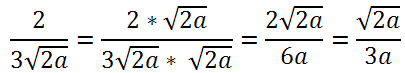
Definzione 5: un’espressione della forma :

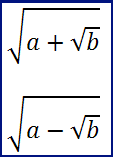
viene chiamata “radicale quadratico doppio” e se   , allora valgono le seguenti uguaglianze:

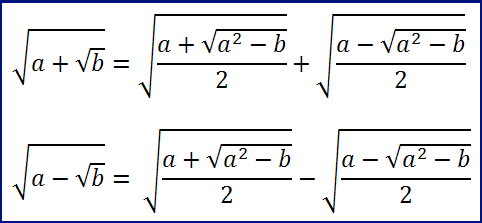
Definizione 6: le potenze frazionarie. Sono nient altro che un altro modo di scrivere un radicale:

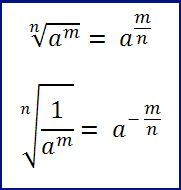
(m,n interi positivi strettamente)

e viceversa: