Disequazioni fratte o frazionarie – Matematica
Disequazioni fratte o frazionarie: come si presentano e come risolverle.
Le disequazioni fratte o frazionarie sono rappresentate dal rapporto di due espressioni in una incognita. L’incognita è presente quindi sia a numeratore che a denominatore:
\( \frac{N(x)}{D(x)}\geq 0\; oppure\; \frac{N(x)}{D(x)}\leq 0 \)o anche:
\( \frac{N(x)}{D(x)}> 0\; oppure\; \frac{N(x)}{D(x)}< 0 \)Questo tipo di disequazioni ti pongono la seguente domanda: “Quando il rapporto fra numeratore e denominatore mi dà valori positivi (o negativi)”? A questa si risponde con lo studio della positività del numeratore N(x) e del denominatore D(x). Ma procediamo con ordine:
- Il denominatore deve essere diverso da zero: D(x) ≠ 0 (CE – campo di esistenza dell’espressione N(x)/D(x)). Nel caso di disequazioni più complesse, come ad esempio contenenti logaritmi, si devono considerare anche altre condizioni). Le disequazioni fratte più semplici sono quelle polinomiali.
- Determino gli zeri o radici del numeratore: N(x)=0. (In genere rappresentano un cambio di segno).
- Determino gli zeri del denominatore: D(x)=0, stando attento acchè nessuno degli zeri ricada fuori dai valori del CE, nel qual caso non si devono prendere in considerazione per scrivere le soluzioni, nel caso di positività o negatività non stretta (≥ , ≤) oppure sono dei valori da escludere dalle soluzioni.
- Determino quando il numeratore è positivo, ovvero pongo N(x)>0 , a prescindere se nella traccia è presente il simbolo <, >, ≤ oppure ≥.
- Determino quando il denominatore è positivo, ovvero pongo D(x)>0 , a prescindere se nella traccia è presente il simbolo <, >, ≤ oppure ≥.
- Metto sotto forma grafica le due disequazioni N(x)>0 e D(x)>0 disegnando i rispettivi intervalli con segno. Le soluzioni delle due rispettive disequazioni mi dicono dove esse sono positive, nella restante parte sono negative ovviamente.
- Poiché N(x)/D(x) è il prodotto tra N(x) * (1/D(x)), disegno una terza grafica con il prodotto dei segni.
- A questo punto la soluzione dell’equazione fratta si trova considerando gli intervalli con il segno richiesto dalla traccia (>,≥ intervalli positivi, viceversa negativi).
Un esempio vale più di mille parole:
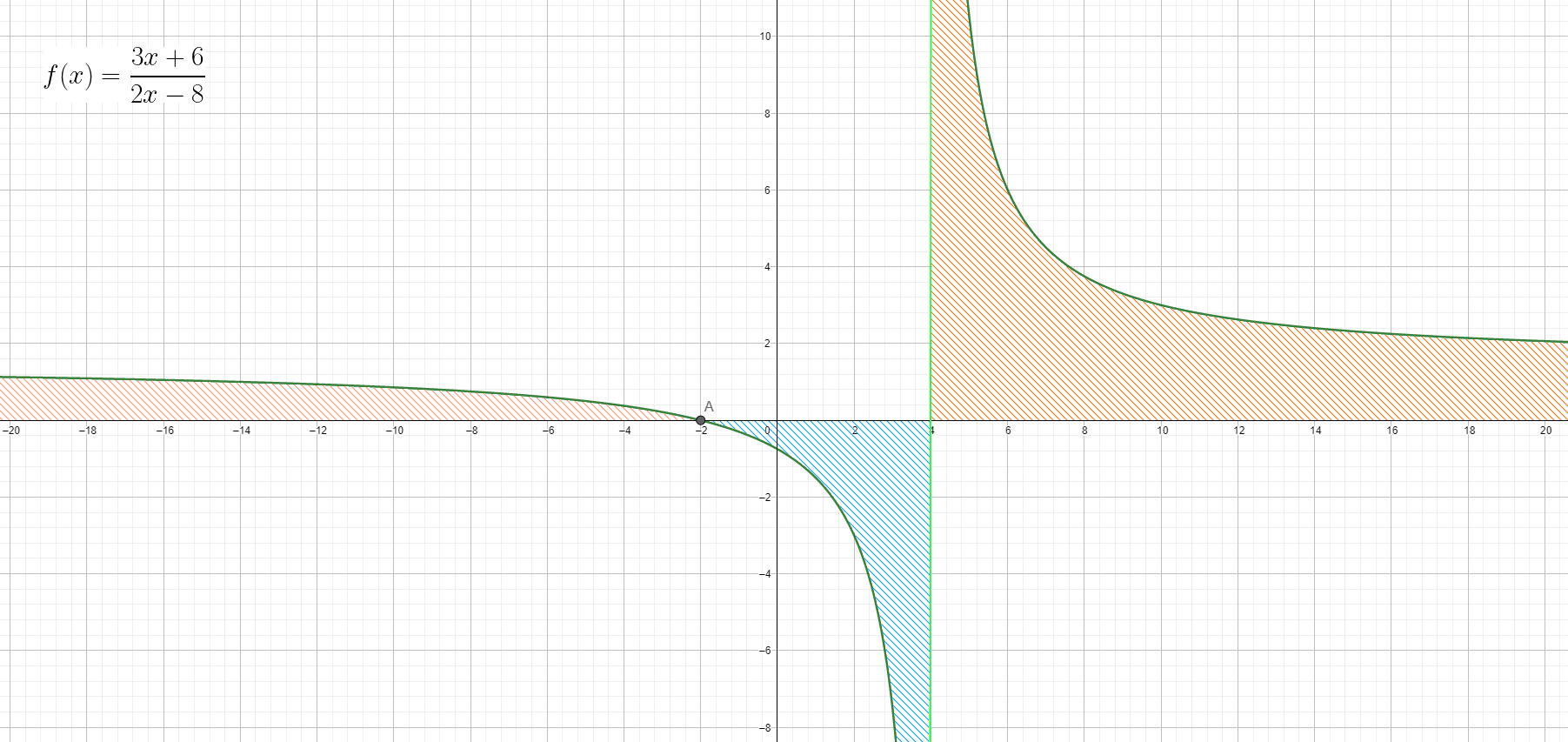
\( \frac{3x+6}{2x-8}>0 \) \( N(x)>0 \rightarrow3x+6>0\rightarrow x>-2 \) \( D(x)>0 \rightarrow 2x-8>0\rightarrow x>4 \) \( D(x)\neq 0 \rightarrow 2x-8\neq 0\rightarrow x\neq 4 \)(Se fosse stata una disequazione fratta con il ≥ avremmo dovuto non considerare il 4 tra le soluzioni)
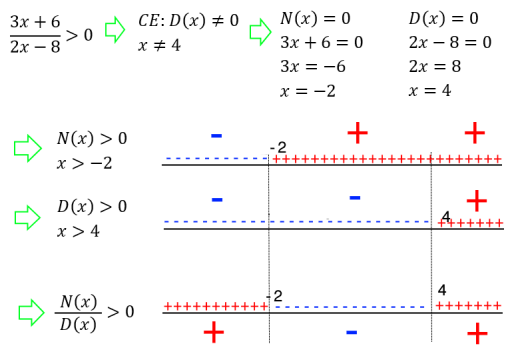
Equazioni Fratte – Esempio 1
Quindi: studio il CE: x≠4; passo a trovare gli zeri del numeratore e denominatore x=-2 e x=4 che mi servono a stabilire quando sono positivi: x>-2 e x>4; effettuo il prodotto dei segni ottenendo la soluzione della disequazione (ovvero la risposta alla domanda di cui sopra) che è S:{ x<-2 v x>4).