Disequazioni fratte con parametro – Matematica
Disequazioni fratte con parametro a numeratore, a denominatore o in entrambi i casi: come si presentano e come risolverle.
Le disequazioni fratte con parametro sono essenzialmente delle disequazioni frazionarie, come si è avuto modo di vedere qui, rappresentate dal rapporto di due espressioni in una incognita. L’incognita è presente sia a numeratore che a denominatore. Nel caso di disequazioni fratte con parametro viene aggiunta una ulteriore difficoltà, rappresentata dalla presenza di un parametro (k, a , m.. ecc).
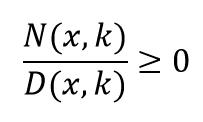
Disequazioni fratte con parametro – Matematica
L’incognita da studiare è sempre la x; il parametro k è comunque un numero reale. Il procedimento per la risoluzione è uguale fondamentalmente: si studia la positività del numeratore N(x,k) e del denominatore D(x,k) e si studia il prodotto dei segni.
- Il denominatore deve essere diverso da zero: D(x,k)≠0 (CE – campo di esistenza dell’espressione N(x,k)/D(x,k)).
- Determino gli zeri del numeratore : N(x,k)=0.
- Determino gli zeri del denominatore : D(x,k)=0, stando attento acchè nessuno degli zeri coincida con i valori del CE, nel qual caso non si deve prendere in considerazione per scrivere le soluzioni nel caso di positività o negatività non stretta (≥ , ≤).
- Determino quando il numeratore è positivo, ovvero pongo N(x,k)>0 , a prescindere se nella traccia è presente il simbolo <, >, ≤ oppure ≥.
- Determino quando il denominatore è positivo, ovvero pongo D(x,k)>0 , a prescindere se nella traccia è presente il simbolo <, >, ≤ oppure ≥.
- Metto sotto forma grafica le due disequazioni N(x,k)>0 e D(x,k)>0 disegnando i rispettivi intervalli con segno.
- Poichè N(x,k)/D(x,k) è il prodotto tra N(x,k) * (1/D(x,k)), disegno una terza grafica con il prodotto dei segni.
- A questo punto la soluzione dell’equazione fratta si trova considerando gli intervalli con il segno richiesto dalla traccia (>,≥ intervalli positivi, viceversa negativi).
Esempio di disequazione fratta con parametro k
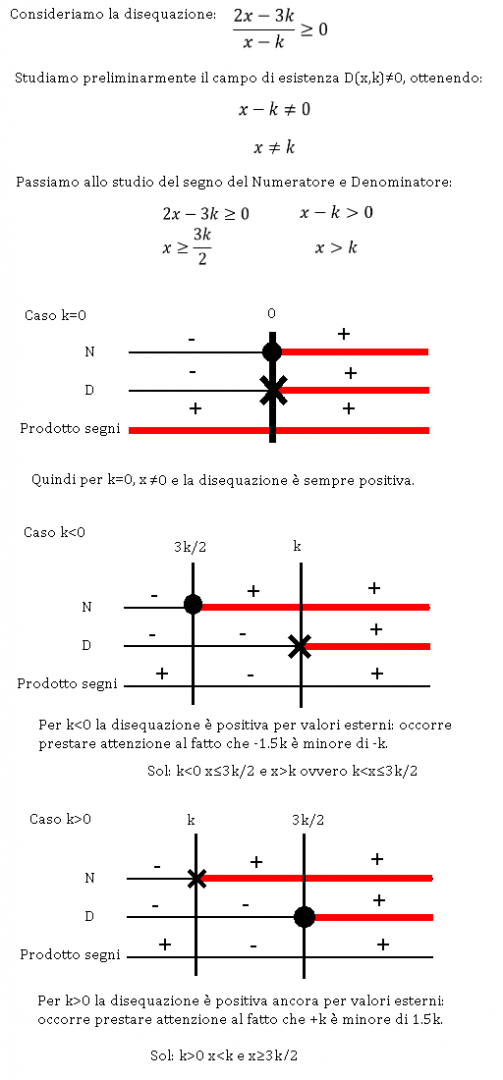
Disequazioni fratte con parametro – Esempio – Matematica
Fondamentale quindi tenere conto della posizione reciproca delle soluzioni di numeratore e denominatore.