Discontinuità di una funzione – Matematica
Punti di discontinuità delle funzioni matematiche a una variabile
Prima di parlare della discontinuità di una funzione matematica a una variabile è bene ricordare cosa si intende per continuità di una funzione in un punto x*. Cercando di dare una definizione molto semplice, si può pensare a una funzione continua come al disegno di una linea sul piano cartesiano “, senza staccare la matita dal foglio”. Se una funzione è continua in un punto, in tale punto il suo grafico non presenta interruzioni.
f:R → R
y=f(x), con x=x*
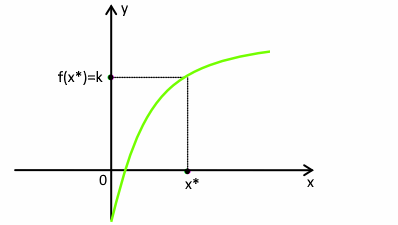
Discontinuità – Funzione continua
La continuità è definita dall’uguaglianza del limite destro e di quello sinistro con il valore che la funzione assume proprio nel punto x*, ovvero:
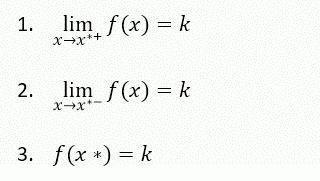
Una funzione si dice continua se è verificata la continuità in ogni punto del suo intervallo di definizione o campo di esistenza. Quando la continuità esiste in tutti i punti di un intervallo, la funzione si dice continua nell’intervallo. In ragione di questo, si parla di funzione discontinua quando le uguaglianze di cui sopra non sussistono. Quindi una funzione che non è continua in un punto si dice discontinua in quel punto.
In particolare si definiscono tre tipologie o specie che rendono discontinua la funzione in un punto:
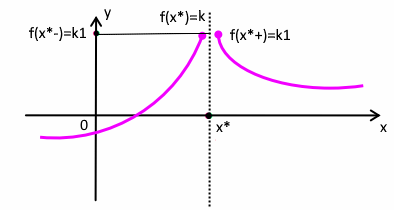
Funzione con discontinuità di prima specie in un punto x*
Si ha un punto discontinuo di prima specie quando esistono finiti i limiti destro e sinistro ma sono diversi tra loro:
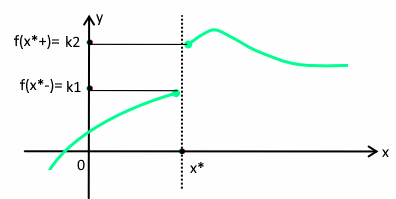
Discontinuità di prima specie
Ricapitolando:
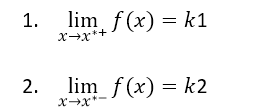
La differenza |k1 – k2 | si dice salto della funzione.
Esempio:
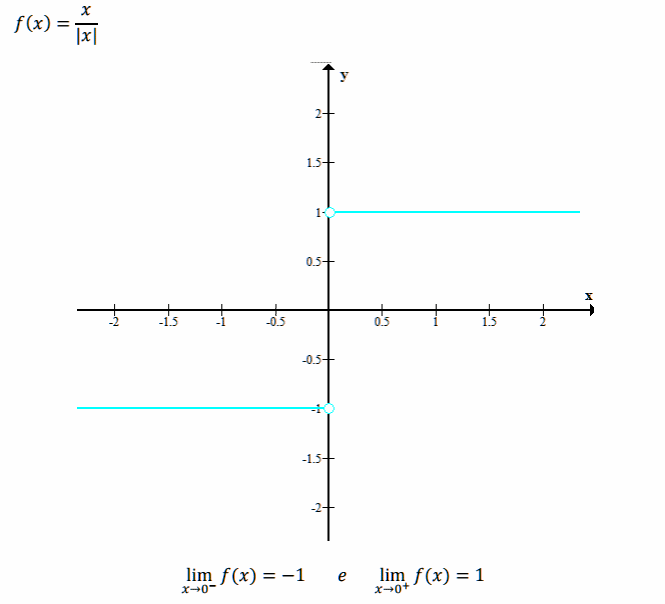
Esempio di discontinuità di prima specie
La funzione “segno di x” ha è discontinua in x*=0, la tipologia è di prima specie. In questo caso il salto è pari a |-1 – 1| = 2.
Funzione con discontinuità di seconda specie in un punto x*
Si ha un punto discontinuo di seconda specie quando almeno uno (quindi anche entrambi) dei due limiti (destro o sinistro) non esiste o tende a infinito:
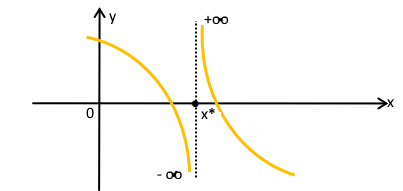
Discontinuità di seconda specie
Ricapitolando i punti fermi da studiare sono (è un esempio teorico):
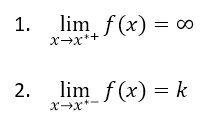
Esempio:
Esempio di discontinuità di seconda specie
Nel punto x*=1 si ha la funzione è discontinua. Nel caso di questa funzione particolare, il limite destro vale -infinito mentre il limite sinistro vale +infinito.
Funzione con discontinuità di terza specie o eliminabile in un punto x*
Si ha un punto discontinuo di terza specie o eliminabile quando esistono finiti e sono uguali i limiti destro e sinistro ma non esiste la funzione in x* oppure se il valore della funzione in x* è diverso dal valore del limite:
Discontinuità di terza specie
Ricapitolando i punti fermi da studiare sono :
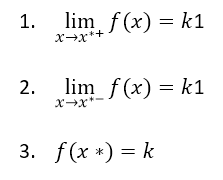
Esempio:
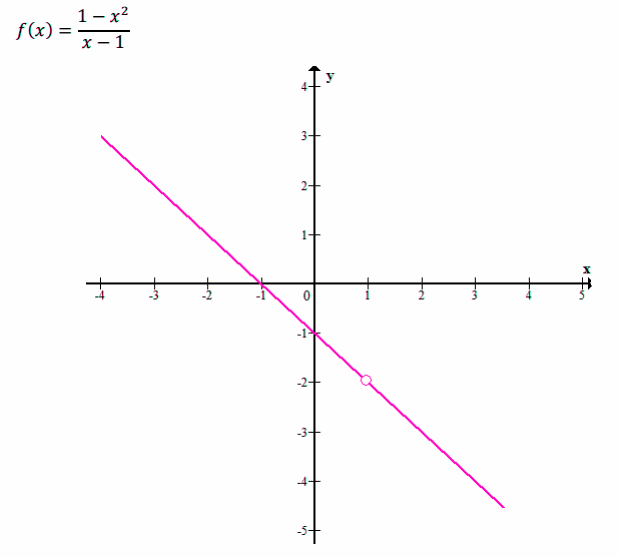
Esempio di discontinuità di terza specie
Nel punto x*=1 si ha la funzione è discontinua. Il salto è nullo. Inoltre la funzione può essere resa continua ripristinando il punto “mancante”.
Note:
Per scoprire la presenza di punti che rendono la funzione discontinua, occorre studiare tutti i punti che non fanno parte del campo di esistenza della funzione, tranne che non siano gli estremi dello stesso.