Retta R137 – Problemi di Geometria Analitica
Retta R137 – Problemi di Geometria Analitica.
Una serie di problemi di geometria analitica risolti durante le ripetizioni date a studenti di Liceo Scientifico, Classico e Ragioneria e del primo anno di università di varie facoltà, presi da vari testi scolastici e tracce. Retta R137 è un problema di difficoltà medio-facile.
[el58862bfc101c9]
Traccia del problema sulla retta R137
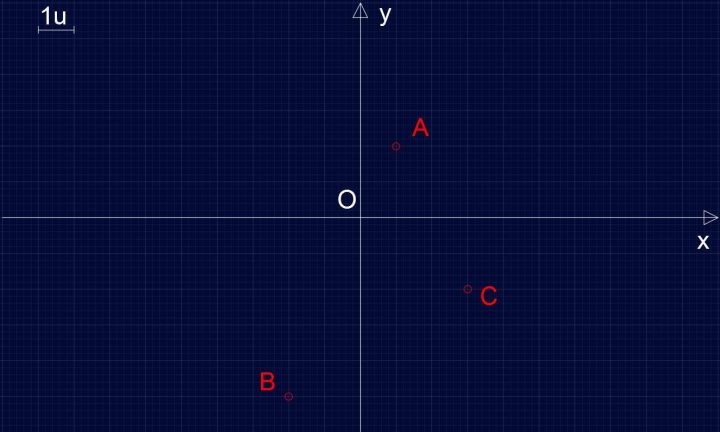
Dati i punti A(1,2); B(-2,-5); C(3,-2), rappresentarli nel piano cartesiano e determinare il Perimetro e l’Area del triangolo ABC.
Dati:
A(1,2); B(-2,-5); C(3,-2)
Svolgimento:
Preliminarmente disegniamo il piano cartesiano, fissiamo l’unità di misura e posizioniamo i punti A, B e C.
Retta R137 – Disegno del piano cartesiano e dei punti del problema
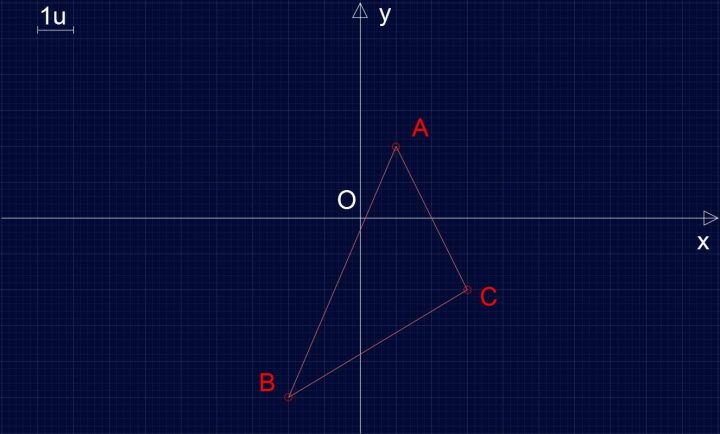
Passiamo quindi a disegnare il triangolo e a calcolare le misure dei lati AB, BC e AC per poi ricavare il perimetro come somma dei lati.
Il calcolo della distanza tra due punti in generale si ottiene dal teorema di Pitagora:
AB = √[(xA-xB)2 + (yA-yB)2] perciò nel nostro caso:
AB = √[(-1-2)2 +(-5-2)2] =√(9+49) =√58 ≅ 7,6
BC = √[(-3-2)2 +(-5+2)2] =√(25+9) =√34 ≅ 5,8
AC = √[(1-3)2 +(2+2)2] =√(4+16) =√20 ≅ 4,5
Il perimetro è quindi P=AB+BC+AC ovvero:
P=√58+√34+√20 ≅ 7,6 + 5,8 + 4,5 ≅ 17,9
Retta R137 – Il triangolo ABC
Purtroppo quello ottenuto non è un triangolo equilatero, ne isoscele e nemmeno rettangolo. (Per quanto riguarda quest’ultima affermazione basta misurare l’angolo C che potrebbe sembrare retto col goniometro o se si ha dimestichezza con la goniometria ricavarlo come funzione inversa della tangente ad esempio; in qualunque caso si ottiene un angolo di 94°).
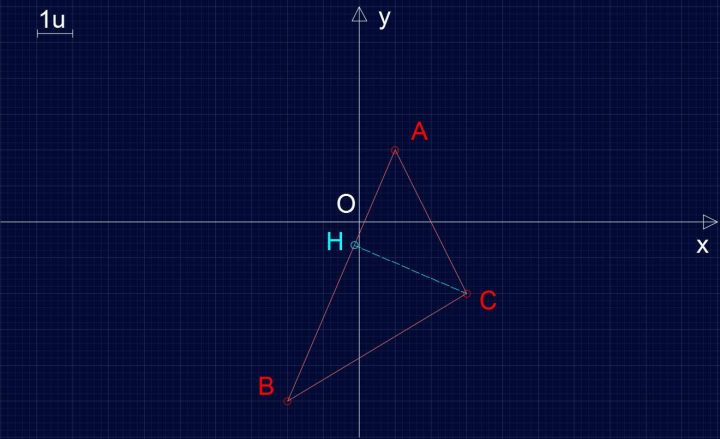
Per quanto riguarda l’Area, essendo quella di un triangolo pari A= (base x altezza)/2, essa non è calcolabile immediatamente, in quanto pur potendo scegliere come base un qualsiasi lato (AB,BC o AC), non conosciamo nessuna altezza ad essi. Per comodità grafica, scelgo come base AB e quindi l’altezza sarà CH.
Retta R137 – Scelta della base e individuazione altezza
Poichè l’altezza deve essere perpendicolare alla base e non conosciamo le coordinate del punto H, l’unica cosa che possiamo fare è tentare di applicare il calcolo “distanza di un punto da una retta”, che è, per come è definita, la minima distanza di un punto da una retta, che, guarda caso, coincide con la distanza misurata perpendicolarmente. Quindi il punto da cui vogliamo calcolare la distanza è C, la retta r sarà necessariamente quella passante per AB. Pertanto ne scriviamo l’equazione, usando l’espressione classica per trovare una retta passante per due punti (A e B in questo caso):
[(y-yA)/(yB-yA)]=[(x-xA)/(xB-xA)]
ricordando che A(1,2) e B(-2,-5), sostituendo:
[(y-2)/(-5-2)]=[(x-1)/(-2-1)] →
(y-2)/(-7) – (x-1)/(-3)=0 →
-3(y-2)+7(x-1)=0 → -3y+6+7x-7=0 →
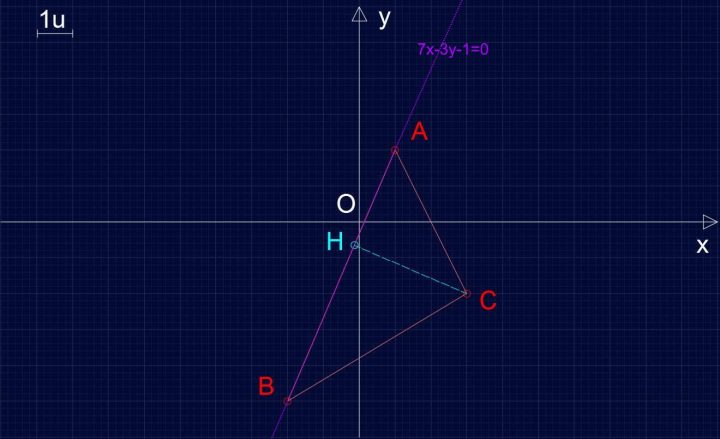
7x-3y-1=0 → r: 7x-3y-1=0
Retta R137 – Distanza retta punto
Applichiamo quindi la regoletta della distanza punto-retta, ricordando che C(3,-2) e che quindi xC = 3 e yC =-2 e che i coefficienti della retta r sono a=7, b=-3 e c=-1:
d(C,r)= |axC+byC+c|/√(a2+b2) = |7· 3 + (-3)·(-2)+(-1)|/√(72+32)=
=|21+6-1|/√(49+9) = 26/√58 ≅ 3,4
d(C,r) = Altezza CH = 26/√58 ≅ 3,4
quindi A = 0.5xABxCH → A=0.5 x √58 x 26/√58 = 13.
E questo è quanto.
