Posizione di una retta rispetto alla parabola
Come stabilire la posizione di una retta rispetto a una parabola.
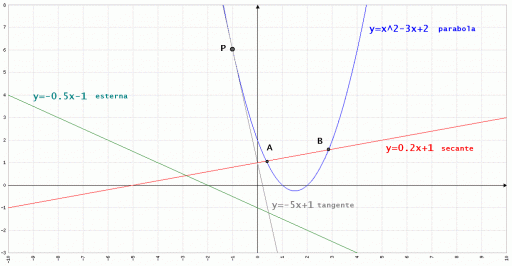
Determinare la posizione di una retta rispetto a una parabola, cioè determinare se è secante, esterna oppure tangente, è semplicissimo. Basta impostare un sistema che contenga le equazioni della retta e della parabola in questione. In base al numero di soluzioni ammesse si potrà stabilire la tipologia. In particolare: se il sistema ammette due soluzioni separate e distinte allora la retta è secante; se il sistema ammette due soluzioni coincidenti la retta è tangente; infine se il sistema non ammette soluzioni allora la retta è esterna. La figura sottostante illustra i tre casi.
Posizione di una retta rispetto alla parabola
La parabola degli esempi seguenti ha equazione y=x²-3x+2.
RETTA SECANTE LA PARABOLA
La retta che già sappiamo essere secante in questo esempio ha equazione y=0.2x+1. Impostiamo il sistema e troviamo le soluzioni: 
Il sistema ammette due soluzioni reali e distinte; vuol dire che ci sono due punti di intersezione. La retta è secante la curva. I punti di intersezione P1 e P2 che si ottengono sostituendo X1 e X2 nell’equazione più semplice (quella della retta) hanno quindi coordinate: 
RETTA TANGENTE ALLA PARABOLA
La retta che già sappiamo essere tangente ha equazione y=-5x+1.
Impostiamo il sistema e troviamo le soluzioni:
Il sistema ammette due soluzioni reali e coincidenti; vuol dire che c’è un punto di intersezione. La retta è tangente alla curva. Il punto di intersezione P3 si ottiene sostituendo X nell’equazione più semplice (quella della retta).
RETTA ESTERNA ALLA PARABOLA
La retta che già sappiamo essere esterna ha equazione y=-0.5x-1. Impostiamo il sistema e troviamo le soluzioni: 
Il sistema non ammette soluzioni; non c’è un punto di intersezione. La retta è esterna alla curva.
Nota:
Data una retta di equazione :
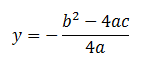
dove a b c sono i coefficienti della conica (parabola in questo caso), questa equazione rappresenta una retta tangente al vertice e perpendicolare all’asse di simmetria della conica
Link utili
- .Le coniche (wikipedia)
