Parabola P103 – Problemi di Geometria Analitica
Parabola P103 – Problemi risolti di Geometria Analitica
Una serie di problemi di geometria analitica risolti durante le ripetizioni date a studenti di Liceo Scientifico, presi da vari testi scolastici. Parabola P103 è un problema di difficoltà medio-alta (se non altro per la sua lunghezza), preso presumibilmente dal testo edito da Zanichelli.
[el58862bfc101c9]
Traccia del problema sulla parabola P103
Data la parabola di equazione x=½ y² -2y e il punto P(-2,3) determinare le rette tangenti t1 e t2 passanti per tale punto. Considerando l’ordinata 1 determinare la tangente t3 per il corrispondente punto sulla parabola (P3). Infine calcolare l’area del triangolo ottenuto dall’intersezione delle tre tangenti trovate. (fonte: presumibilmente Zanichelli – Matematica)
Dati:
\(Parabola: \\ x=\frac{1}{2}y^2-2y \\ Punto: P(-2;3) \)
Soluzione:
FASE 1. Si inizia anzitutto a disegnare il grafico della parabola, che ha l’asse parallelo all’asse delle ascisse (y=0), attraverso il vertice V( -Δ/4a, -b/2a) che risulta essere V(-2,2) e le sue intersezioni con gli assi cartesiani: x=0 ⇒ y1=4 e y2=0; ottenendo i punti P1(0,4) e P2(0,0). Viene inoltre rappresentato il punto P(2,3), noto.
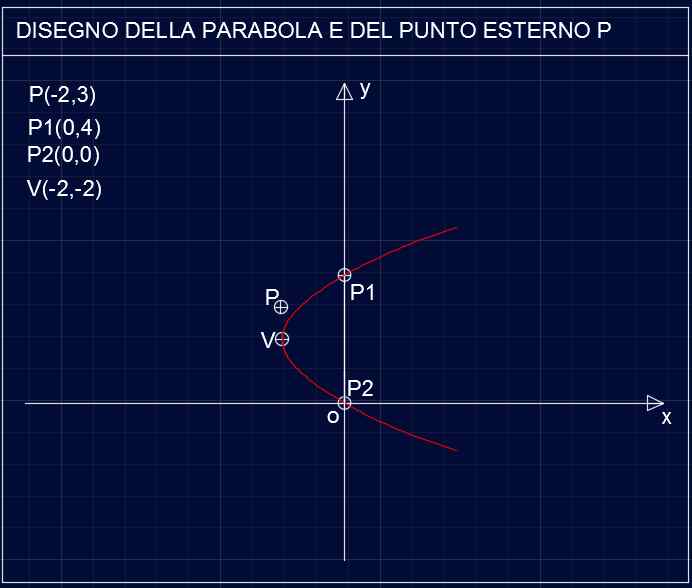
Parabola P103 – Disegno della conica e del punto P
FASE 2. Per determinare le equazioni delle rette tangenti uscenti dal punto P, si procede con il metodo classico: 1) equazione del fascio proprio di rette di centro P e 2) sistema fascio-conica, dal quale si ottiene un’equazione risolvente in m (coefficiente angolare da determinare). Si deve imporre la condizione di tangenza, ovvero che il Δ=b²-4ac=0
- y-(3) = m (x-(-2) ⇒ x = (y + 3 – 2m)/m con m≠0
- (y + 3 – 2m) = ½ my² -2my
Svolgendo le varie operazioni si ottiene l’equazione risolvente:
½ my² – y(4m+2) + (4m+6)=0
dove:
a=m; b=-(4m+2); c= (4m+6);
e quindi il Δ:
Δ= -8m+4=0 ⇒ m=½
perciò la tangente t2 è: x-2y+8=0
Per quanto riguarda la tangente t1 occorre osservare che il punto P e V hanno stessa ascissa, per cui l’unica retta che può essere tangente è t1: x=-2.
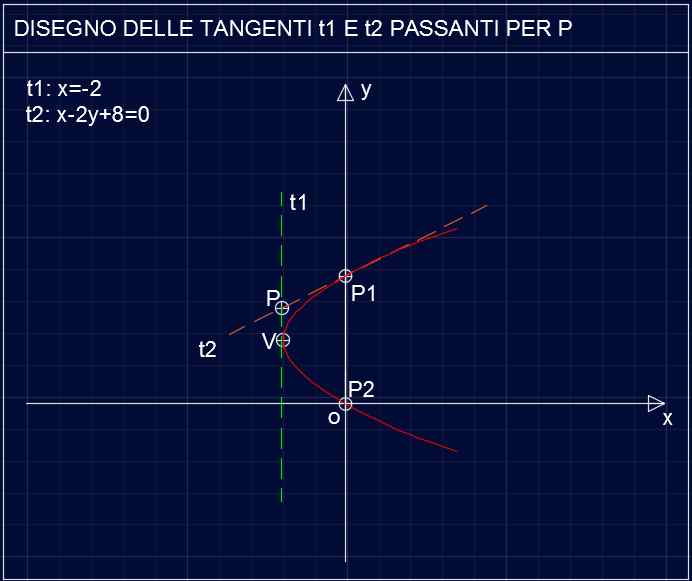
Parabola P103 – Tangenti t1 e t2 passanti da P
FASE 3. Occorre ora determinare il punto P3 sulla conica di ordinata yP3=1 e determinare la retta tangente alla parabola per tale punto. Quindi se yP3=1 ⇒ xP3= -3/2 cioè P3(-3/2,1).
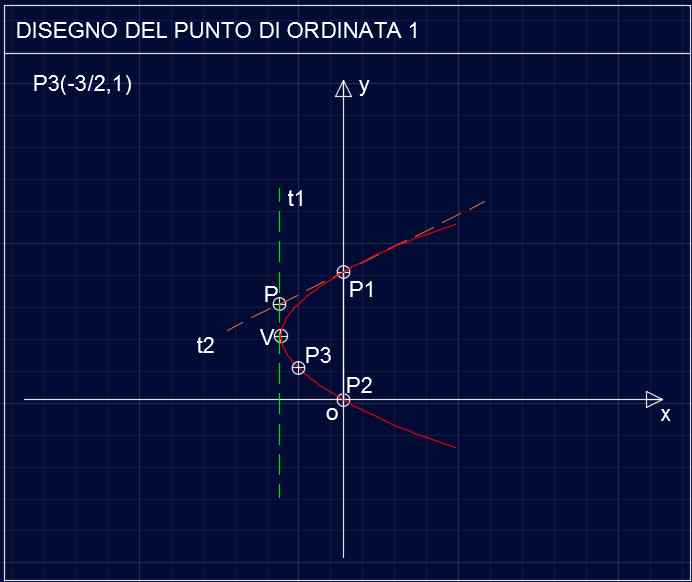
Parabola P103 – Punto P3
FASE 4. In questo caso si può procedere come nella fase 2 precedente e mettere a sistema fascio di rette con centro in P3 e parabola, ricavando il coefficiente angolare m, imponendo Δ=0. (In alternativa si può usare il metodo del coefficiente angolare scrivendo l’equazione del fascio con centro in P3 essendo m = 2 a (xP3) + b).
- y-(1) = m (x-(-3/2) ⇒ 2x = (2y -2 – 3m)/m con m≠0
- (2y -2 – 3m) = my² -4my
Svolgendo le varie operazioni si ottiene l’equazione risolvente:
my² – 2y(4m+1) + (2m+3)=0
dove:
a=m; b=-2(4m+1); c= (2m+3);
e quindi il Δ:
Δ=m² + 2m + 1=0 ⇒ m=-1
perciò la tangente t3 è: x-2y+8=0
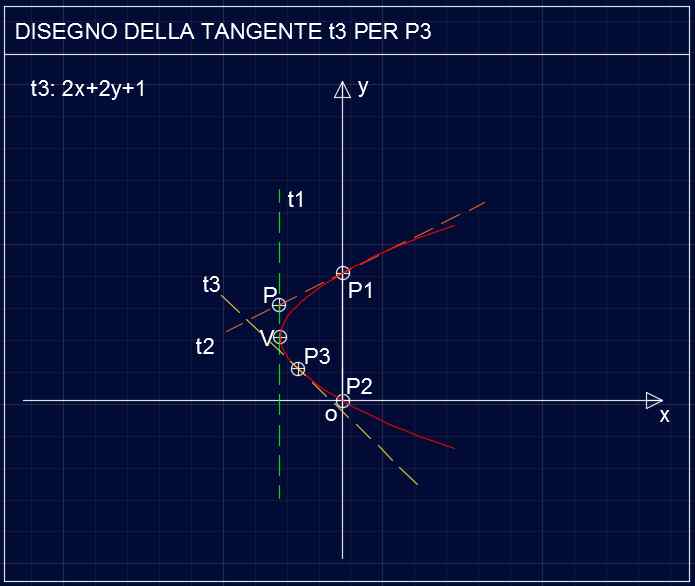
Parabola P103 – Tangente t3
FASE 4. A questo punto troviamo tutti i punti di intersezione tra le tangenti t1 t2 e t3 e calcoliamo l’area del triangolo PAB:
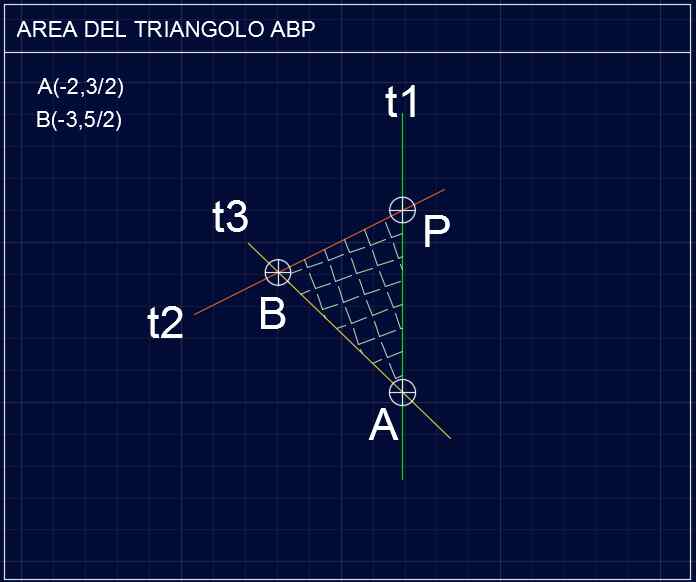
Parabola P103 – Triangolo PAB – Ingrandimento
Intersecando t1 e t2 riottengo P(-1,3); intersecando t1 con t2 ovvero mettendo a sistema le due equazioni ottengo il punto A(-2,3/2); infine mettendo a sistema t2 e t3 ottengo il punto B(-3,5/2).
Scelgo AP come base del triangolo la cui dimensione è semplicemente:
b= (3-3/2)=3/2
L’altezza del triangolo la si calcolo come la distanza tra retta t1 e punto P:
h=|-2-2|/1 = 4
Area=0,5bh=3
Link utili:
- La geometria analitica (wikipedia)
- La parabola su Romoletto Blog (vedi)