Integrali indefiniti II004 – Analisi Matematica
Integrali indefiniti II004 – Analisi Matematica
Una serie di integrali indefiniti di Analisi Matematica svolti per l’ultimo anno di Scuola Superiore o per il primo anno di Università, presi dalle ripetizioni date a studenti di Liceo Scientifico/Classico e Istituti Tecnici e a matricole universitarie. Integrali indefiniti II004 è di difficoltà bassa, ma completo di tutti i passaggi.
Traccia di Integrali indefiniti II004
Risolvere il seguente integrale:
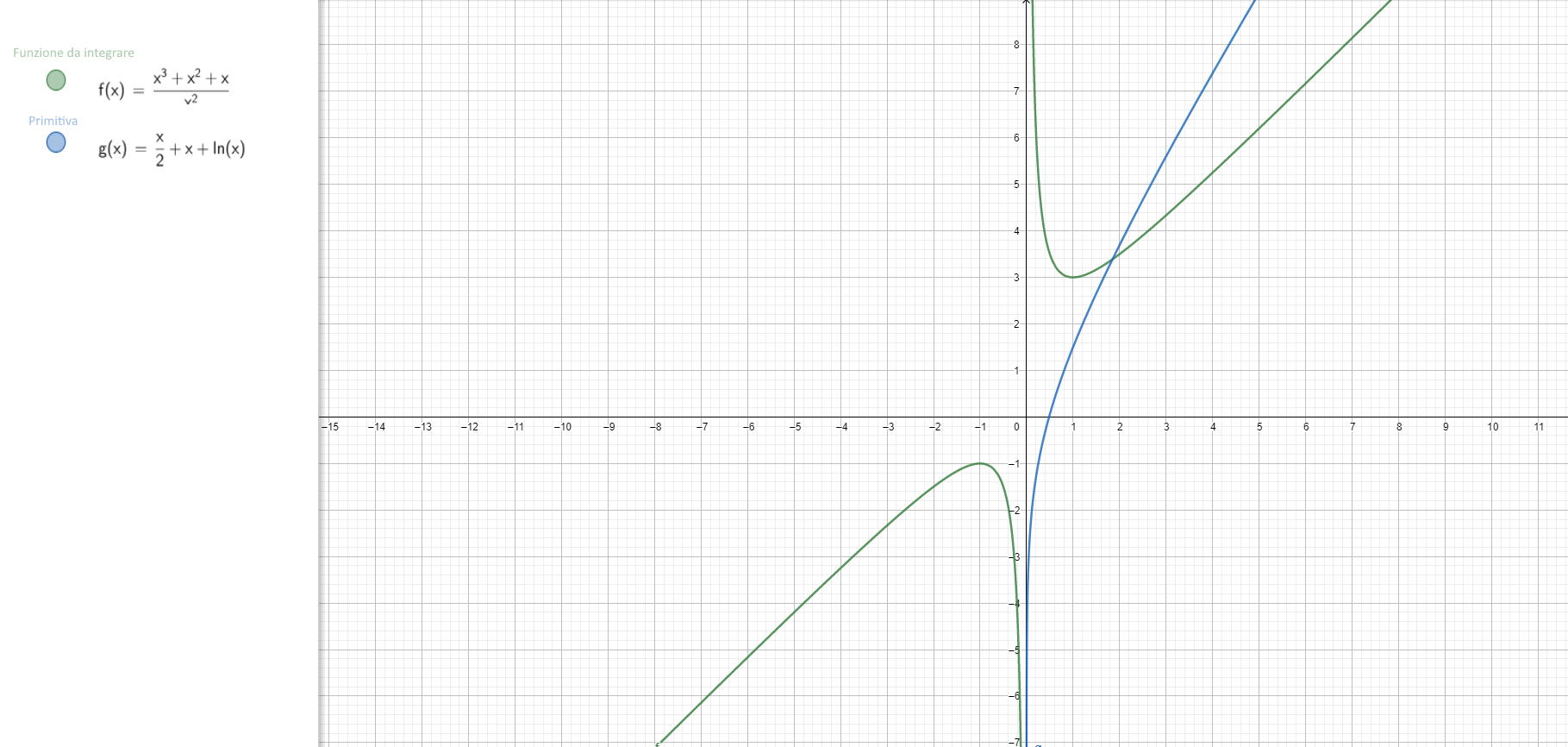
\( \int \frac{x^3+x^2+x}{x^2}\: dx;\)
Svolgimento
Integrale indefinito di f(x)=(x^3+x^2+x)(x^-2) – Grafico della funzione – II004
Cominciamo a scrivere diversamente l’integrale di partenza spezzandolo in una somma di integrali e svolgiamo i semplici passaggi:
\(\int \frac{x^3+x^2+x}{x^2}\: dx=\) \(=\int \frac{x^3}{x^2}\: dx+\int \frac{x^2}{x^2}\: dx+\int \frac{x}{x^2}\: dx=\)semplifichiamo,
\(=\int x\: dx+\int dx+\int \frac{1}{x }\: dx=\) \( =(\frac{1}{2}x^2+c1)+(x+c2)+(ln(x)+c3)= \) \( =\frac{1}{2}x^2+x+ln(x)+c \)E questo è quanto, salvo errori o omissioni.
Link utili:
- Integrali indefiniti (Wikipedia)
