Circonferenza C173 – Problemi di Geometria Analitica
Circonferenza C173 – Problemi risolti di Geometria Analitica
Una serie di problemi di geometria analitica risolti durante le ripetizioni date a studenti delle superiori e del primo anno di università di varie facoltà e presi da vari testi scolastici. Circonferenza C173 è un problema di difficoltà medio-alta.
[el58862bfc101c9]
Traccia del problema sulla Circonferenza C173
Dati il punto P(0;3) e il punto B(-2;1) appartenente alla retta r di equazione 11x-3y+25=0, tangente ad una circonferenza γ passante per il punto P, determinare l’equazione di γ. Calcolare poi la tangente alla circonferenza nel punto D di ascissa 3 e di ordinata positiva. (Fonte: presumibilmente Zanichelli – Matematica)
Dati:
P(0;3), B(-2;1) ∈ γ (γ circonferenza). Tangente in B alla circonferenza r: 11x-3y+25=0.
Soluzione:
Quesito 1)
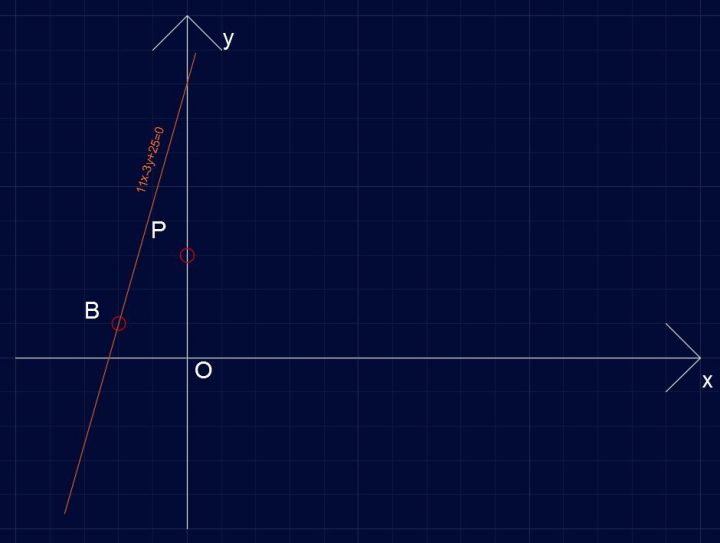
Circonferenza C173 – dati
L’equazione generica di una circonferenza è del tipo:
x2+y2+ax+by+c=0
che dipende quindi dai valori di a, b, c che perciò devono essere in qualche modo determinati. Poichè sappiamo che P ∈ γ e che anche B ∈ γ (in quanto è un punto di tangenza) allora possiamo già scrivere due equazioni:
P(0;3) → (0)2+(3)2+a(0)+b(3)+c=0
B(-2;1) → (-2)2+(1)2+a(-2)+b(1)+c=0
Ce ne manca una terza per avere un sistema di tre equazioni in tre incognite e poter quindi determinare a,b e c. La terza equazione la ricaviamo osservando che la retta tangente in B ha coefficiente angolare:
mr=-a/b → mr= 11/3
Poichè il raggio della circonferenza è sempre perpendicolare alle tangenti e in particolare a quella in B, allora il coefficiente angolare di una retta passante per B e per il centro C (ignoto) della circonferenza sarà:
ms= -1/mr → ms = -3/11
Il coefficiente angolare ms si ricava essendo C(xC; yC) o per comodità notativa C(α;β) dove, per definizione:
α=-a/2 e β=-b/2
per cui si avrà:
ms= Δy/Δx = (yB-yC)/(xB-xC) =
sostituendo:
ms= (1-β)/(-2-α) = (1+b/2)/(-2+a/2) = -3/11
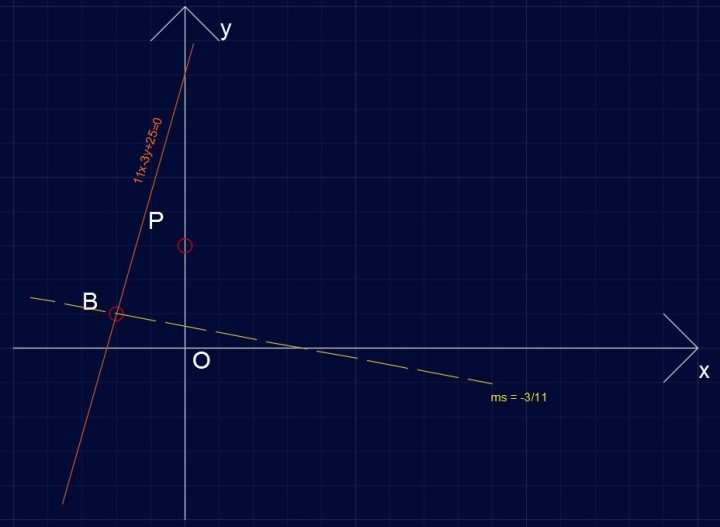
Circonferenza C173 – coefficiente angolare
Le tre equazioni a sistema, svolti un po’ di passaggi, saranno quindi:
/ 9+3b+c=0
< 5-2a+b+c=0
\ 11b+3c+10=0
Il sistema, risolto fornisce:
a=-3/2; b=-1/2; c=-15/2.
L’equazione della circonferenza sarà quindi:
x2+y2 – (3/2)x-(1/2)y-(15/2)=0
2x2+2y2 – 3x-y-15=0
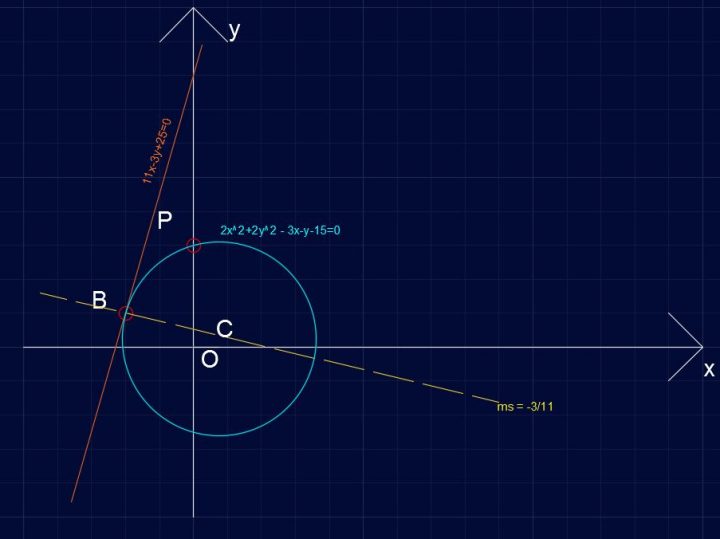
Quesito 2)
Determiniamo il punto D(3; yD). Non conosciamo infatti l’ordinata. Procediamo quindi sostituendo 3 al posto della x nell’equazione della circonferenza appena trovata:
2(3)2+2y2 – 3(3)-y-15 = 0
18+2y2 – 9-y-15 = 0
2y2 – y + 6 = 0
Abbiamo ottenuto una equazione di secondo grado, che ci darà due soluzioni di cui una sarà positiva e sarà quella da scegliere, come richiesto dalla traccia. Risolvendola:
Δ=b2+4ac → Δ=1+48=49 → √Δ=7
y1,2=(1±7)/4
y1=-3/2 e y2=2
quindi D(3,2).
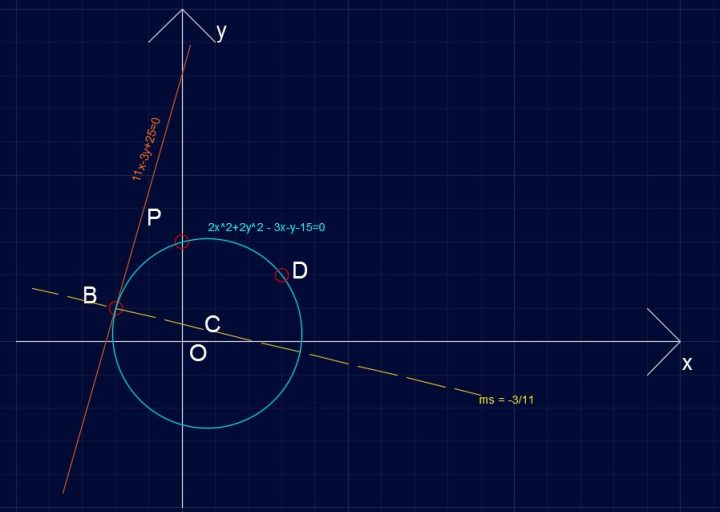
Circonferenza C173 – punto D
La tangente a un punto sulla circonferenza si ricava costruendo un fascio di rette con centro nel punto desiderato (D in questo caso) e cercando il coefficiente angolare della retta contenente il raggio in quel punto (r=CD in questo caso), ricordando sempre che tangente e raggio sono sempre perpendicolari. Occorrono le coordinate di C(α;β) dove, per definizione α=-a/2 e β=-b/2.
α=3/4 e β=1/4 → C(¾; ¼)
Calcolo il coefficiente angolare:
C(¾; ¼); D(3,2)
mD= Δy/Δx = (yD-yC)/(xD-xC) → mD=7/9
A noi serve :
mt=-1/mD → mt=-9/7
L’equazione del fascio con centro in D è:
y-yD = mt(x-xD)
quindi sostituendo:
y-2 = -(9/7)(x-3)
9x+7y -41 = 0
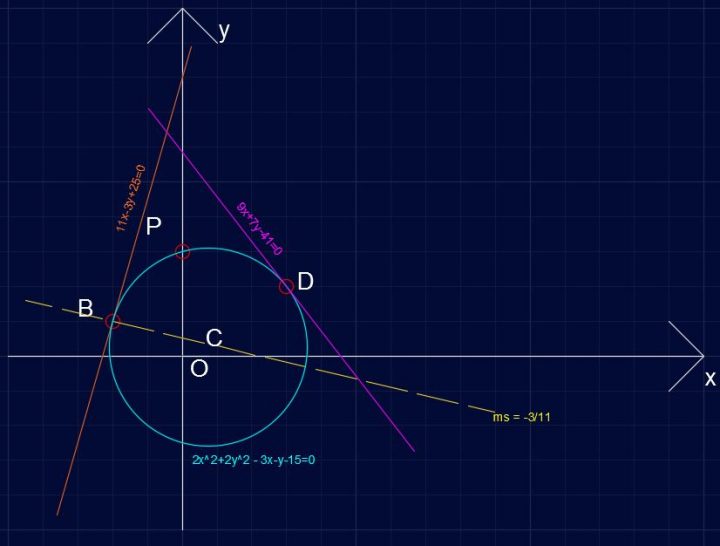
Circonferenza C173 – tangente in D