Analisi Matematica – Paniere Ecampus – AM016-02

Una serie di problemi e quesiti di Analisi Matematica risolti durante le ripetizioni date a studenti del primo anno di università di varie facoltà di Ingegneria, presi dal paniere Ecampus – Ingegneria Industriale. Analisi Matematica – AM016-02 è un quesito di difficoltà medio-bassa.

Traccia del problema di Analisi Matematica – AM016-02

Il limite per x che tende a π/2 di tan x(1-sin x):
1) vale +∞ o -∞;
2) non esiste;
3) vale 1;
4) vale 0.

Soluzione

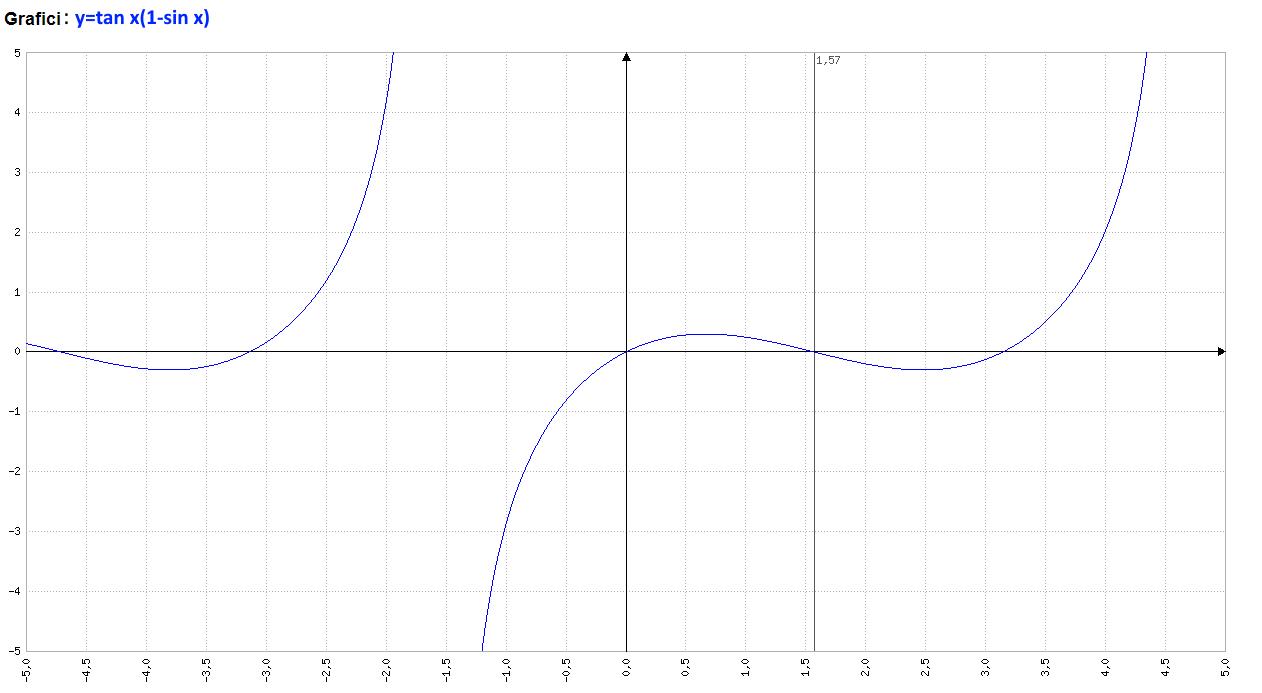
Analisi Matematica – f(x)=tan x(1-sin x)  – Grafico della funzione – AM016-02

Questo limite ricade, cosi com’è, nella forma indeterminata ∞ • 0:

Romoletto Blog ti consiglia...

Nespresso De'Longhi Pixie EN127.S, Macchina da Caffè con Sistema Capsule, Modalità ECO, Espresso e Caffè Lungo, Design Compatto, Pressione 19 Bar, 1260W, Silver

Veloce e potente: goditi il caffè aromatico in pochi secondi grazie alla pompa ad alta pressione da 19 bar e al sistema di riscaldamento rapido. Piccola e pratica: il design compatto e il funzionamento intuitivo rendono pixie una compagna ideale ...

Nota: prodotto fornito da Amazon

Lim   tan x(1-sin x) =
x→π/2
= ∞ (1 – 1) = ∞•0

Conviene a questo punto ci ricordare alcuni limiti notevoli:

1. Lim   (1-cos x)/x² = 1/2 
   x→0
2. Lim   (1-cos x)/x = 0 
   x→0
3. Lim  (sen x)/x = 1 
   x→0

che potrebbero esserci utili. Poiché ci serve che il limite tenda a zero, effettuiamo un cambio di variabile e poniamo:

t = π/2 – x;
x = π/2 – t.

Sostituiamo quindi:

Lim  (tan(π/2 – t)(1 – sen(π/2 – t)) =
t→0

Usando le proprietà di seno e coseno:

cos (π/2 – t) = sin(t);
sin (π/2 – t) = cos(t);

= Lim  ctan(t)(1 – cos(t)) =
t→0

Dividiamo e moltiplichiamo per t:

= Lim  t cos(t)(1 – cos(t))/(t sin(t))=
t→0

(lo spezziamo nel prodotto di due limiti)

1. Lim  t · cos(t)/sin(t)=
   t→0
   = Lim  cos(t)/(sin(t)/t) =
   t→0
   = 1/1=1;
2. Lim (1 – cos(t))/t = 0.
   t→0

Pertanto, usando i limiti notevoli 2) e 3) otteniamo che:

Lim   tan x(1-sin x) = A· B=0.
x→π/2

E questo è quanto, salvo errori od omissioni.

Link utili:

• Limite di funzione (Wikipedia)
• Limiti notevoli (Wikipedia)
• UniEcampus (Sito ufficiale)

Elenco AM Ecampus

[el5f806349973d5]