Analisi Matematica – Paniere Ecampus – AM006-02

by Romoletto Blog · 11 Ottobre 2020

Analisi Matematica – Paniere Ecampus – AM006-02

Una serie di problemi e quesiti di Analisi Matematica risolti durante le ripetizioni date a studenti del primo anno di università di varie facoltà di Ingegneria, presi dal paniere Ecampus – Ingegneria Industriale. Analisi Matematica – AM006-02 è un quesito di difficoltà bassa.

Traccia del problema di Analisi Matematica – AM006-02

La funzione f(x)=e^-|x|+cos(x) è:
1) dispari;
2) non simmetrica e non periodica;
3) periodica;
4) pari.

Risposta corretta:

La risposta 4) è VERA.

Soluzione

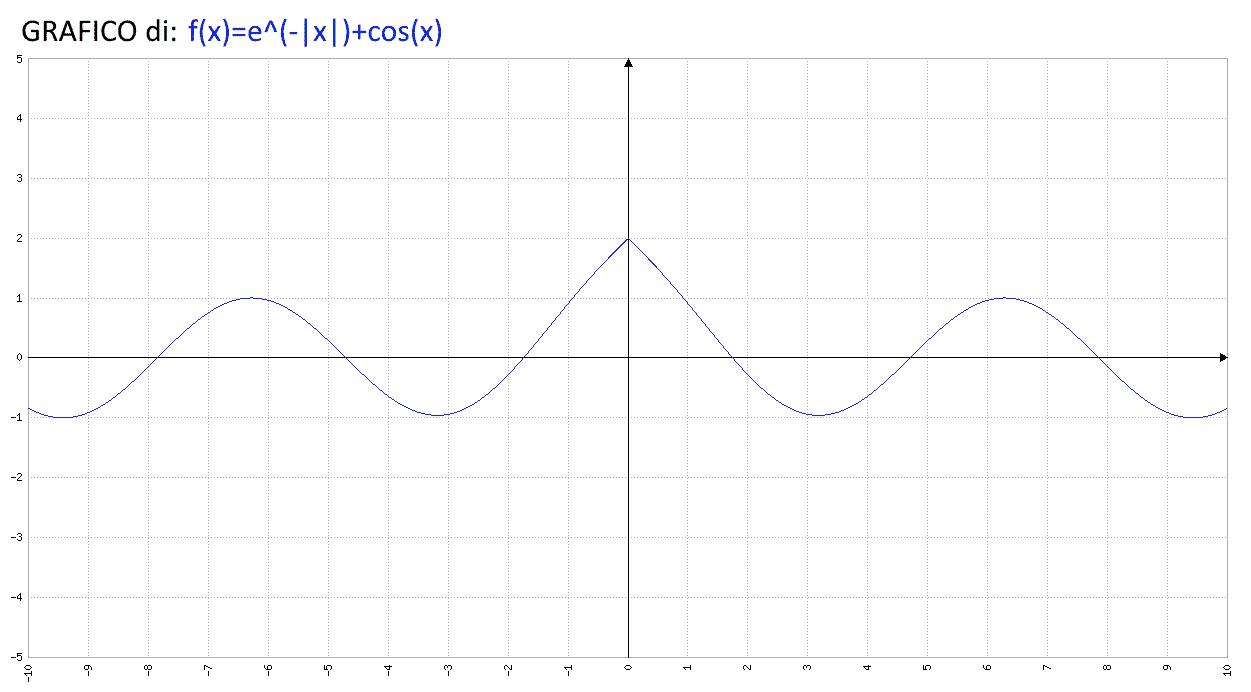
Analisi Matematica – f(x)=e(-|x|)+cos(x) – Grafico della funzione – AM006-02

La risposta 1) è FALSA. Come si vede dai calcoli successivi, la funzione è simmetrica solo rispetto all’asse delle ordinate, pertanto non è dispari.

Per la soluzione procediamo con ordine:

Romoletto Blog ti consiglia...

PESOFORMA CHOCO SMOOTHIE, Pasto Sostitutivo per il Controllo del Peso, Smoothie Gustoso che Aiuta a Rimettersi in Forma, Ricco in Proteine e Fibre, Solo 205 Calorie, 20 pasti, 540 gr

Pesoforma pasto sostitutivo: per rimettersi in forma e in maniera equilibrata utilizza 2 pasti sostitutivi al giorno al posto della colazione e del pranzo oppure della colazione e della cena, preparando lo smoothie con due misurini di polvere e 250ml ...
Nota: prodotto fornito da Amazon

1) Una funzione è dispari se:

∀x∈R, -f(-x)=f(x)
(che è lo stesso che dire f(-x) = – f(x)).

Nel nostro caso i calcoli sono identici a quelli svolti per la 2-a.B e pertanto non è dispari.

La risposta 2) è FALSA. Come si vede dai calcoli successivi, la funzione è simmetrica rispetto all’asse delle ordinate, ma non è periodica.

Per la soluzione procediamo con ordine:

2-a) Quando una funzione è simmetrica? In genere le simmetrie ricercate sono rispetto all’asse delle ordinate e rispetto all’origine.

se ∀x∈R, f(-x)=f(x) → la funzione è simmetrica rispetto all’asse delle ordinate;
se ∀x∈R, f(-x) = – f(x) → la funzione è simmetrica rispetto all’origine;

Quindi:

f(-x) = e^-|-x|+cos(-x) =
= f(x)= e^-|x|+cos(x) ?
Conviene per semplicità controllare addendo per addendo:
e^-|-x|+cos(-x) = e^-|x|+cos(x)
e^-|-x| = e^-|x|? si; evidentemente |-x| = |x|;
cos(-x) = cos(x)? si; (cos è una funzione pari e simmetrica risp. asse ord.);
Pertanto è simmetrica rispetto all’asse delle ordinate.
f(-x) = e^-|-x|+cos(-x) =
= -f(x) = – e^-|x|– cos(x) ?
Conviene per semplicità controllare addendo per addendo:
e^-|-x|+ cos(-x) = – e^-|x|– cos(x)
e^-|-x| = – e^-|x| ? no; (cambia il segno);
cos(-x) = – cos(x) ? no; (cambia il segno).
Pertanto non è simmetrica rispetto all’origine.

2-b) E’ una funzione è periodica di un certo periodo T ?

Per essere funzione periodica deve accadere che essa si ripeta indefinitamente a intervalli regolari (periodi); si deve verificare che:

∃T∈R+ / f(x+T) = f(x)

Nel nostro caso f(x)=e^-|x|+cos(x) è composta da una funzione periodica (il coseno) e da una non periodica e, sopratutto, non lineare. (Esistono dei teoremi che dimostrano la periodicità della somma prodotto quoziente di costanti con una funzione periodica, ma non come somma di funzioni non periodiche con funzioni periodiche). Pertanto la funzione non è periodica.

La risposta 3) è FALSA. Non è periodica di periodo per quanto visto sopra.

Per la soluzione procediamo con ordine:

3) Identica risposta dell’ 2-b: non è una funzione periodica.

La risposta 4) è VERA. E’ simmetrica rispetto all’asse delle ordinate, pertanto è pari.

Per la soluzione procediamo con ordine:

4) Una funzione è pari se:

∀x∈R, f(x)=f(-x).

Nel nostro caso i calcoli sono identici a quelli svolti per rispondere alla 2-a.A e la funzione è pari.

Note

Sempre nell’ottica della maggiore velocità di esecuzione, questa volta si può partire cercando di rispondere alla domanda 2) ovvero verificando se la funzione è simmetrica, in modo da risolvere anche la questione del pari o dispari e passando poi a vedere se è periodica o meno.

E questo è quanto, salvo errori e/o omissioni.