Analisi Matematica – Paniere Ecampus – AM006-01

by Romoletto Blog · 10 Ottobre 2020

Analisi Matematica – Paniere Ecampus – AM006-01

Una serie di problemi e quesiti di Analisi Matematica risolti durante le ripetizioni date a studenti del primo anno di università di varie facoltà di Ingegneria, presi dal paniere Ecampus – Ingegneria Industriale. Analisi Matematica – AM006-01 è un quesito di difficoltà bassa.

Traccia del problema di Analisi Matematica – AM006-01

La funzione f(x)=1+cos(4x)+tan(2x) è:
1) non simmetrica, periodica di periodo π;
2) dispari, periodica di periodo π;
3) pari, periodica di periodo π/2;
4) non simmetrica, periodica di periodo π/2.

Risposta corretta:

La risposta 4) è VERA.

Soluzione

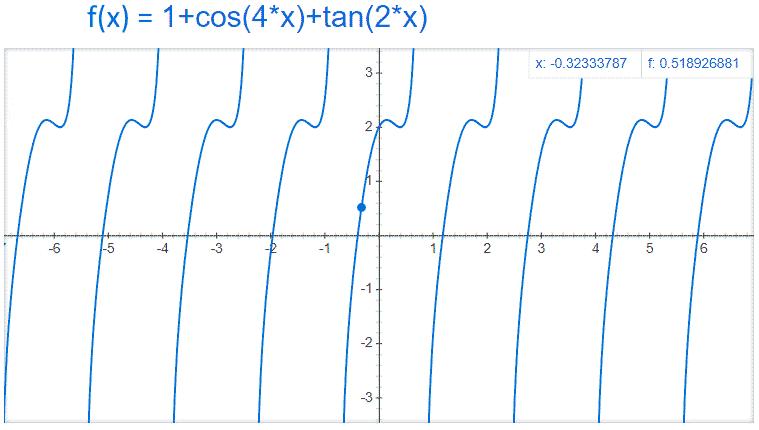
Analisi Matematica – f(x)=1+cos(4x)+tan(2x) – Grafico della funzione – AM006-01

La risposta 1) è FALSA. Non è simmetrica e non è periodica di periodo T=π. (Possiamo pensare subito che la risposta corretta sia la 4) in quanto la funzione, non simmetrica, non è pari, non è dispari.

Per la soluzione procediamo con ordine:

Romoletto Blog ti consiglia...

ProLon – Kit Dieta Mima Digiuno – Programma Nutrizionale di 5 Giorni – Prof. Valter Longo – Autofagia - Made in Italy – Varietà 3 (Piselli, peperoni, lenticchie, ceci)

[imita il digiuno] - prolon offre una modalità sicura e semplice per imitare i benefici del digiuno prolungato in soli 5 giorni, attivando processi rigenerativi come l'autofagia.. [cosa contiene] - il kit prolon contiene una varietà di zuppe, barrette alle ...
Nota: prodotto fornito da Amazon

1-a) Quando una funzione è simmetrica? In genere le simmetrie ricercate sono rispetto all’asse delle ordinate e rispetto all’origine.

se ∀x∈R, f(-x)=f(x) → la funzione è simmetrica rispetto all’asse delle ordinate;
se ∀x∈R, f(-x) = – f(x) → la funzione è simmetrica rispetto all’origine;

Quindi:

f(-x) = 1+cos(-4x)+tan(-2x) =
= f(x) =1+cos(4x)+tan(2x) ?
Conviene per semplicità controllare addendo per addendo:
1=1? si;
1+cos(-4x)+tan(-2x) = 1+cos(4x)+tan(2x)
cos(-4x) = cos(4x)? si; (cos è una funzione pari e simmetrica risp. asse ord.);
~~1+cos(-4x)~~+tan(-2x) = ~~1+cos(4x)~~+tan(2x)
tan(2x)=tan(-2x)? no. (tan è una funzione dispari);
Pertanto non è simmetrica rispetto all’asse delle ordinate.
f(-x) = 1+cos(-4x)+tan(-2x) =
= -f(x) = -1 – cos(4x) – tan(2x) ?
Conviene per semplicità controllare addendo per addendo:
1+cos(-4x)+tan(-2x) = -1-cos(4x)-tan(2x)
1=-1 ? no;
cos(-4x) = -cos(4x)? no;(cos è una funzione pari);
tan(-2x)=-tan(2x)? si; (tan è una funzione dispari).
Pertanto non è simmetrica nemmeno rispetto all’origine.

1-b) Quando una funzione è periodica di periodo π?

Per essere funzione periodica deve accadere che essa si ripeta indefinitamente a intervalli regolari (periodi); si deve verificare che:

∃T∈R+ / f(x+T) = f(x)

Nel nostro caso T=π, pertanto a x dobbiamo aggiungere π:

f(x+T) = 1+cos(4(x+π)) + tan(2(x+π)) =
= f(x) = 1+cos(4x)+tan(2x) ?
Conviene per semplicità controllare addendo per addendo:
1=1? si;
1+cos(4(x+π)) + tan(2(x+π)) =
= 1+cos(4x)+tan(2x)
Usiamo le formule di addizione/sottrazione:
cos(4x+4π)) = cos(4x)cos(4π) – ~~sin(4x)sin(4π)~~ = cos(4x) ? si;
tan(2x+2π)) = (tan(2x) + ~~tan(2π)~~)/(1 – ~~tan(2x) tan(2π)~~) = tan(2x) si;
Pertanto è una funzione periodica di periodo T=π.

Analisi Matematica – Formule di addizione e sottrazione angoli – AM006-01

La risposta 2) è FALSA. Non è dispari e non è periodica di periodo T=π.

Per la soluzione procediamo con ordine:

2-a) Una funzione è dispari se:

∀x∈R, -f(-x)=f(x)
(che è lo stesso che dire f(-x) = – f(x)).

Nel nostro caso i calcoli sono identici a quelli svolti per la 1-a.B e pertanto non è dispari.

2-b) Identica risposta dell’ 1-b: è una funzione periodica di periodo T=π.

La risposta 3) è FALSA. Non è simmetrica, ma è periodica di periodo T=π/2.

Per la soluzione procediamo con ordine:

3-a) Una funzione è pari se:

∀x∈R, f(x)=f(-x).

Nel nostro caso i calcoli sono identici a quelli svolti per rispondere alla 1-a.A e la funzione non è pari.

3-b) Vediamo la periodicità rispetto a T=π/2:

f(x+T) = 1+cos(4(x+π/2)) + tan(2(x+π/2)) =
= f(x) = 1+cos(4x)+tan(2x) ?
Conviene per semplicità controllare addendo per addendo:
1=1? si;
1+cos(4x+2π) + tan(2x+π) =
= 1+cos(4x)+tan(2x)
cos(4x+2π) = cos(4x)cos(2π) – ~~sin(4x)sin(2π)~~ = cos(4x) ? si;
tan(2x+π) = (tan(2x) + ~~tan(π)~~)/(1 – ~~tan(2x) tan(π)~~) = tan(2x) si;
Pertanto è una funzione periodica di periodo T=π/2.

La risposta 4) è VERA. Non è simmetrica ed è periodica di periodo T=π/2.

Per la soluzione procediamo con ordine:

4-a) Vedi i calcoli del punto 1-a.A e 1-a.B;
4-b) Vedi i calcoli del punto 3-b;

Pertanto non è simmetrica ed è periodica di π/2.

Note

Nell’ottica della rapidità di esecuzione (il test dura un’oretta), per dare la risposta non è necessario ovviamente effettuare tutti i calcoli. Partendo dalla non simmetria rispetto all’asse delle ordinate e rispetto all’origine (il che esclude che la funzione sia pari e anche che sia dispari – punti 1-a.A e 1-a.B) si possono subito escludere la 1) la 2) e la 3). L’unica VERA è quindi la 4), senza nemmeno necessità di calcolare la periodicità.

Dai calcoli è venuto fuori che la funzione è periodica sia di π che π/2. Ovviamente questo succede perchè essi sono multipli. Chiaramente per dire qual è la periodicità della funzione occorre prendere il più piccolo periodo entro cui essa si ripete. In questo caso π/2. C’è un modo per calcolare il periodo T a priori? Si, in pratica ogni funzione trigonometrica ha il suo periodo: es. SenX e CosX sono periodici di 2π; TanX è periodica di π. e cosi via. Quindi abbiamo nel nostro caso:

cos(4x) → cos(4(x+kT)) = cos (4x+2πk) →
4x+4kT = 4x +2πk →
4kT=2πk → periodo T₁ → 4T₁=2π da cui T₁=2π/4 = π/2.
tan(2x) → periodo T₂ → 2T₂=π da cui T₂ = π/2.

In generale il periodo di funzioni somma potrebbe essere dato dal minimo comune multiplo tra i periodi trovati, in questo caso T= π/2. (Sempre da verificare, magari numericamente). Da ricordare che la somma di due funzioni periodiche non è necessariamente periodica.

E questo è quanto, salvo errori e/o omissioni.