Retta R103 – Problemi di Geometria Analitica
Retta R103 – Problemi di Geometria Analitica.
Una serie di problemi di geometria analitica risolti durante le ripetizioni date a studenti di Liceo Scientifico, Classico e Ragioneria e del primo anno di università di varie facoltà, presi da vari testi scolastici e tracce di compiti in classe. Retta R103 è un problema di difficoltà media.
[el58862bfc101c9]
Traccia del problema sulla retta R103
Studiare la natura del fascio di rette:
(2+k)x + (k-1)y + 3 – k=0 e determinare k in modo che:1) la retta passi per il punto P(0;2)
2) la retta sia parallela all’asse x
3) la retta sia perpendicolare alla retta passante per A(-1;0) e B(2,-3)4) la retta formi un angolo di 45° con l’asse x.
Svolgimento:
Per indagare sulla natura del fascio di rette in questione è sufficiente ripristinare le due rette che lo hanno prodotto, ovvero:
(2+k)x + (k-1)y + 3 – k=0
2x+kx+ky-y+3-k=0
(2x-y+3)+k(x+y-1)=0
Le rette cercate sono:
r:(2x-y+3)=0
r’:(x+y-1)=0
Per discernere se si tratta di un fascio proprio o improprio abbiamo due vie: la prima è di controllare solo tramite confronto di coefficienti se le due rette sono parallele o incidenti; la seconda è quella di mettere a sistema le due rette e se otteniamo soluzione (centro del fascio) allora si tratta di fascio proprio. Eseguiremo entrambe.
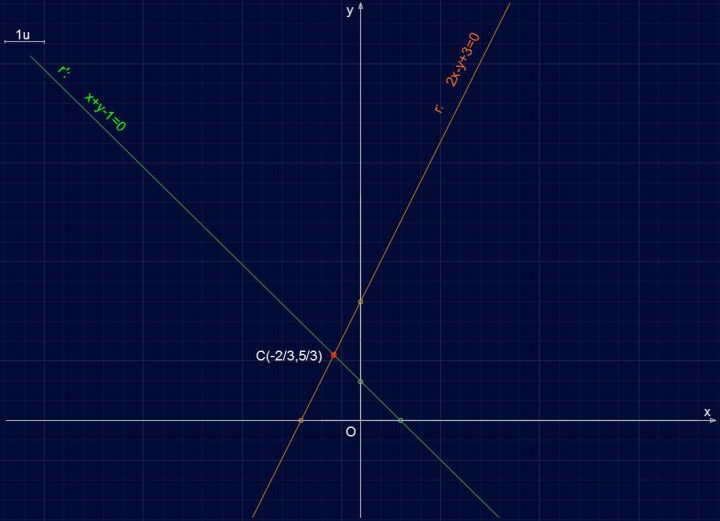
Retta R103 – Piano cartesiano, Fascio di rette proprio e centro del fascio
- 1) Controlliamo la seguente espressione: p=ab’-a’b. Se p=0 ⇒ rette parallele ⇒ Fascio Improprio; se p≠0 ⇒ rette incidenti ⇒ Fascio Proprio. Nel nostro caso a,b,c sono i coefficienti della retta r; a’,b’,c’ sono i coefficienti della retta r’. Quindi: 2*1-1*(-1)=2+1=3≠0 ⇒ rette incidenti ⇒ Fascio Proprio.
- 2) Come detto, mettiamo a sistema le due rette:
/ 2x-y+3=0
<
\ x+y-1=0
/ -3y+5=0
<
\ x=1-y
/ y=5/3
<
\ x=-2/3
Il centro del fascio è C(-2/3;5/3) e quindi le rette sono incidenti e il fascio è proprio.
Quesito 1) la retta passi per il punto P(0;2)
Tra tutte le rette del fascio proprio di centro C, devo trovare quella che passa anche il punto P dato, particolarizzando k. In questo caso, poiché lo scopo dell’esercizio è solo conoscere il valore di k basta sostituire le coordinate Px e Py nell’equazione del fascio: (2+k)x + (k-1)y + 3 – k=0 ovvero (2+k)*Px + (k-1)*Py + 3 – k=0 ottenendo una equazione lineare da cui ricavare k.
(2+k)Px + (k-1)Py + 3 – k=0 ; P(0;2)
(2+k)*0+(k-1)*(-2)+3-k=0
2k-2+3-k=0
k=-1
Volendo si può sostituire il valore di k nell’equazione del fascio per ottenere anche l’equazione della retta s: passante per C e P:
(2+k)x + (k-1)y + 3 – k=0 ; k=-1
(2-1)x + (-1-1)y + 3 -(-1)=0
x-2y+4=0
s: x-2y+4=0
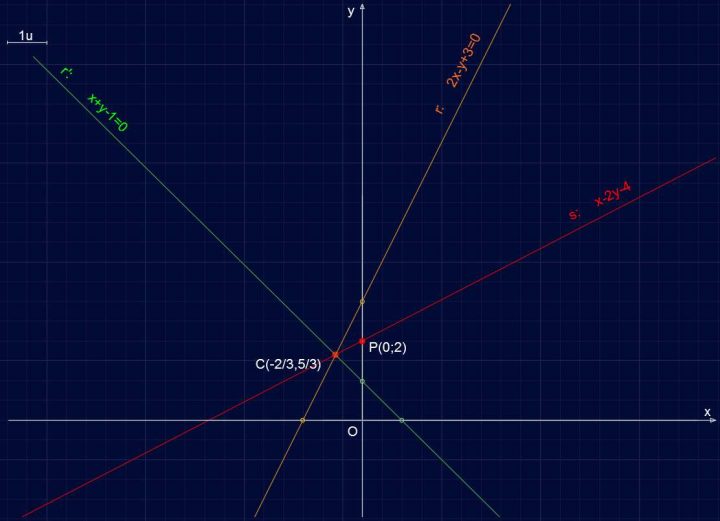
Retta R103 – Retta passante per P(0;2)
Quesito 2) la retta sia parallela all’asse x
Affinchè la retta cercata sia parallela all’asse x occorre che il suo coefficiente angolare sia nullo ovvero mt =-a/b = 0. Nel nostro caso:
(2+k)x + (k-1)y + (3 – k)=0
a=(2+k); b=(k-1); c=(3-k)
mt= -(2+k)/(k-1) =0
k≠1;
-2-k=0 ⇒ k=-2
Volendo si può sostituire il valore di k nell’equazione del fascio per ottenere anche l’equazione della retta t: passante per C e parallela a x:
(2+k)x + (k-1)y + 3 – k=0 ; k=-1
(2-2)x + (-2-1)y + 3 -(-2)=0
-3y+5=0
t: -3y+5=0
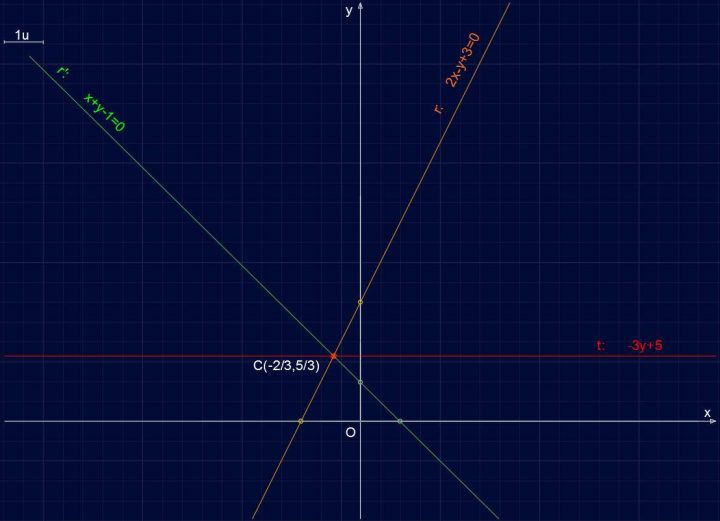
Retta R103 – Retta parallela all’asse x
Quesito 3) la retta sia perpendicolare alla retta passante per A(-1;0) e B(2,-3)
La condizione di perpendicolarità tra due rette è espressa dalla relazione di antireciprocità dei rispettivi coefficienti angolari. Nel nostro caso deve essere:
mu = – 1/mAB
Ricordiamo inoltre che sempre il coefficiente angolare di una equazione è espresso dalla relazione:
mu =-a/b
e che, avendo due punti, il coefficiente angolare si calcola come:
mAB=Δy/Δx = (yB-yA)/(xB-xA)
Quindi sostituendo otteniamo rispettivamente, essendo:
(2+k)x + (k-1)y + (3 – k)=0
a=(2+k); b=(k-1); c=(3-k)
mu =-(2+k)/(k-1)
A(-1;0), B(2,-3)
mAB=(-3-0)/(2+1)= -1
mAB=-1
quindi:
mu = – 1/mAB
-(2+k)/(k-1)=(-1)/(-1)
-(2+k)/(k-1)=1
k≠1;
-2-k-k+1=0
k=-1/2
k= -1/2
Volendo si può sostituire il valore di k nell’equazione del fascio per ottenere anche l’equazione della retta u: passante per C e parallela a x:
(2+k)x + (k-1)y + 3 – k=0 ; k=-1
(2-1/2)x + (-1/2-1)y + 3 -(-1/2)=0
3x/2-3/2y+7/2=0
u: 3x-3y+7=0
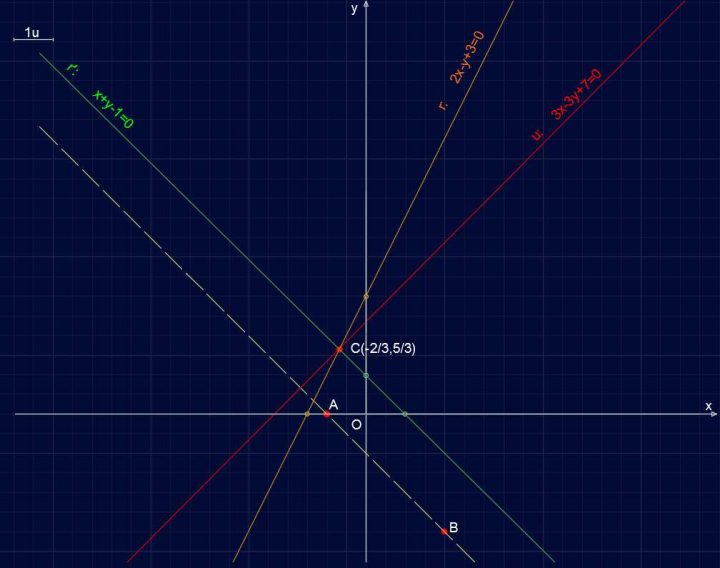
Retta R103 – Retta perpendicolare al segmento AB
Quesito 4) la retta formi un angolo di 45° con l’asse x
Tra tutte le rette di centro C mi serve quella che forma un angolo di 45° con l’asse x ovvero mi occorre una retta di coefficiente angolare mv=1. Al solito quindi sostituendo otteniamo, essendo:
(2+k)x + (k-1)y + (3 – k)=0
a=(2+k); b=(k-1); c=(3-k)
mv =-(2+k)/(k-1)
mv=1
1=-(2+k)/(k-1)
k≠1;
k-1+2+k=0
k=-1/2
Volendo si può sostituire il valore di k nell’equazione del fascio per ottenere anche l’equazione della retta v: passante per C e parallela a x:
(2+k)x + (k-1)y + 3 – k=0 ; k=-1
(2-1/2)x + (-1/2-1)y + 3 -(-1/2)=0
3x/2-3/2y+7/2=0
v: 3x-3y+7=0
Otteniamo quindi la stessa retta del punto 3). E questo è quanto.