Parabola P421 – Problemi di Geometria Analitica
Parabola P421 – Problemi risolti di Geometria Analitica
Una serie di problemi di geometria analitica risolti durante le ripetizioni date a studenti delle superiori e del primo anno di università di varie facoltà e presi da vari testi scolastici. Parabola P421 è un problema di difficoltà media.
[el58862bfc101c9]
Traccia del problema sulla parabola P421
Dati i punti A(0;5), B(2;2), C(6;2) appartenenti a una parabola con asse di simmetria parallelo all’asse delle Y:
1) determinarne l’equazione; 2) scrivere l’equazione della tangente alla parabola in A; 3) trovare l’area del triangolo formato dall’intersezione dellla predetta tangente con gli assi cartesiani. (Fonte: presumibilmente Zanichelli – Matematica)
Dati:
A(0;5), B(2;2), C(6;2) ∈ γ (γ parabola ad asse di simmetria verticale).
Soluzione:
Rappresentiamo sempre tutti i dati nel piano cartesiano, in modo da avere un’idea di massima di quello che si andrà a fare.
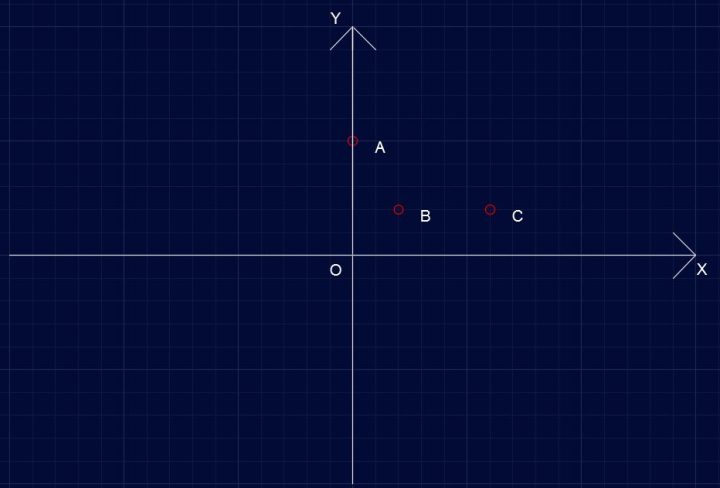
Parabola P421 – Rappresentazione dei dati
Fase 1: Equazione della parabola
L’equazione generica di una parabola ad asse di simmetria verticale (parallelo all’asse Y) è del tipo:
y = ax2 + bx + c
Per determinarla occorre quindi quantificare i parametri a, b, c. Per fare questo basta imporre l’appartenenza dei tre punti A, B e C alla parabola in questione, sostituendo semplicemente le coordinate e ottenendo cosi un sistema di tre equazioni in tre incognite.
A(0;5) ⇒ 5 = a(0)2 + (0)b + c
B(2;2) ⇒ 2 = a(2)2 + (2)b + c
C(6;2) ⇒ 2 = a(6)2 + (6)b + c
ovvero:
/ c – 5 = 0
< 4a + 2b + c – 2 = 0
\ 36a + 6b +c – 2 = 0
Risolvendolo si ottiene:
a = ¼; b = -2; c = 5.
per cui la parabola cercata è:
y = ¼x2 – 2x + 5
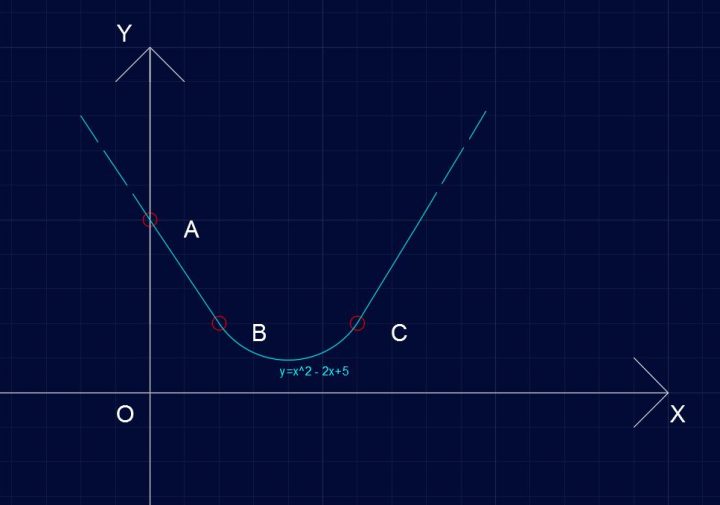
Parabola P421 – Equazione della parabola
Fase 2: Tangente al punto A
Nota l’equazione della parabola, andiamo a determinare la tangente in A. Scriviamo l’equazione del fascio di rette con centro in A e determiniamo quale coefficiente angolare attribuirle per ottenere la retta tangente.
y-yA=mt (x -xA)
A(0,5)
y-5=mx
y=mx+5
A questo punto occorre mettere a sistema l’equazione del fascio con l’equazione della parabola; poiché vogliamo che il punto di contattato sia solo il punto A, il determinante della cosiddetta equazione risolvente deve essere nullo: Δ = 0.
/ y=mx+5
<
\ y = ¼x2 – 2x + 5
Sostituendo la prima nella seconda si ottiene:
x2-(8+4m)x=0
Il determinante deve essere:
Δ = b2 – 4ac = (8+4m)2 – 4(0)= 0
8+4m = 0 ⇔ m= -2
quindi il coefficiente angolare cercato è m=-2, che ci fa ottenere la tangente cercata:
y=-2x+5
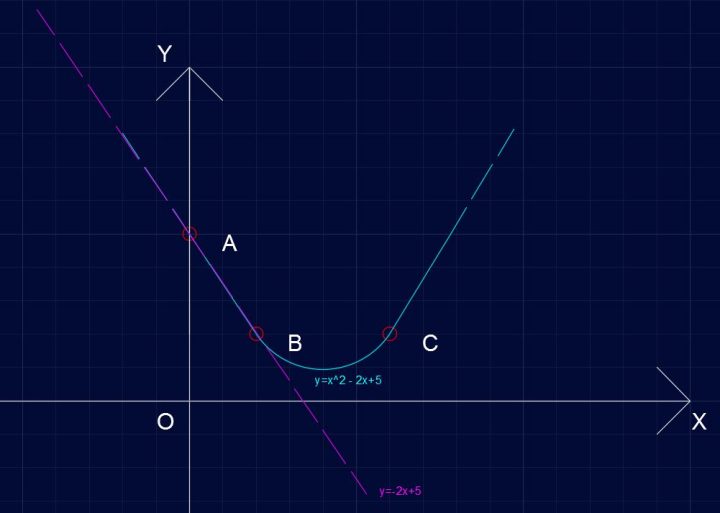
Parabola P421 – Equazione della tangente in A
Fase 3: Area del triangolo AOD
Per determinare le coordinate del punto D e quindi per ottenere le dimensioni del triangolo AOD, basta fare sistema tra la retta tangente e l’asse delle X. Quindi:
/ y=-2x+5
<
\ y=0
-2x=-5 → x = 5/2
Le coordinate di D sono quindi D(0; 5/2). Il triangolo AOD ha base OD=5/2 e altezza OA = 5 da cui:
Area= (OD x OA)/2 → Area = 25/4
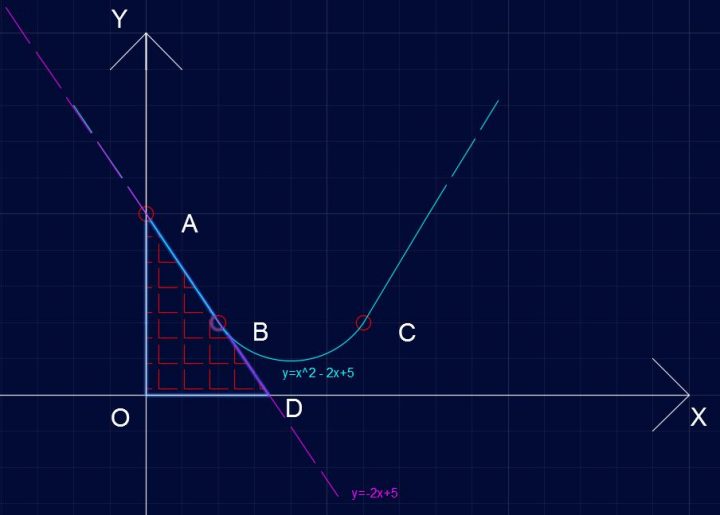
Parabola P421 – Area del triangolo AOD
E questo è quanto.
Link utili:
- La geometria analitica (wikipedia)
- La parabola su Romoletto Blog (vedi)