Decimali in frazioni: come trasformarli
Trasformare i numeri decimali in frazioni: come si fa?
Spesso viene richiesto dagli esercizi dei vari testi di matematica di trasformare i numeri decimali nelle corrispondenti frazioni. Le regolette da seguire sono al solito poche e semplici. Verranno illustrate direttamente con esempi.
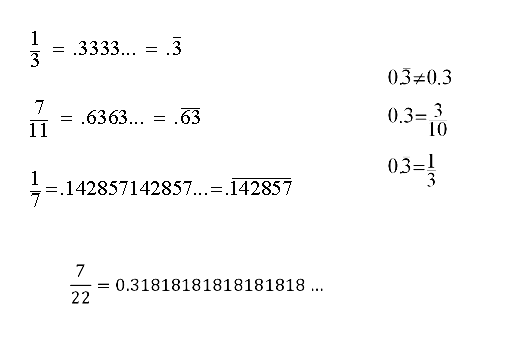
Trasformare decimali in frazioni
- Esempio: 7,5 è un numero decimale limitato.
Per trasformarlo nella frazione generatrice, scriviamo l’intero numero, senza virgola. Al numeratore si ha quindi: 75 ,mentre al denominatore si deve inserire un 1 e tanti zeri quanti sono le cifre dopo la virgola. In questo caso ne abbiamo una cifra quindi, la frazione generatrice è: 75/10 ovvero semplificando per 5: 15/2. - Esempio: 0,6 è un numero periodico semplice, infatti non abbiamo l’antiperiodo. La frazione generatrice si forma in questo modo: il numeratore è dato dall’intero numero, senza la virgola, a cui sottraiamo tutto ciò che non fa parte del periodo: 6-0; al denominatore dobbiamo inserire tanti 9 quante sono le cifre che compongono il periodo: 6/9 ovvero semplificando per 3: 2/3.
- Esempio: 0,63 : in questo caso il numero decimale è periodico misto perchè c’è almeno una cifra decimale non periodica. Per determinare la frazione generatrice, scriviamo il numero senza virgola al numeratore. Sottraiamo l’antiperiodo: (63 – 6) e al denominatore inseriamo tanti 9 quanti sono le cifre che compongono il periodo e tanti zeri quante sono le cifre dell’antiperiodo. In questo caso: 57/90 possiamo ridurre la frazione dividendo per 3 ottenendo 19/30.
Altri esempi:
- Esempio: 1,47 : è un numero decimale periodico semplice, perché non abbiamo antiperiodo. Al numeratore inseriamo l’intero numero senza virgola, e sottraiamo tutto ciò che non fa parte del periodo: (147 – 3). Al denominatore inseriamo tanti 9 quante sono le cifre del periodo (in questo caso 2): 144/99; possiamo ridurre la frazione dividendo per 3 ottenendo:16/11.
- Esempio 3,236 .Questo è un numero periodico misto perché è presente l’antiperiodo. Scriviamo tutto il numero senza virgola al numeratore, sottraiamo tutto ciò che non fa parte del periodo: 3236-32. Al denominatore, inseriamo tanti 9 quante sono le cifre del periodo (in questo caso 2) e tanti zeri quante sono le cifre dell’antiperiodo (in questo caso una): 3204/990. Possiamo semplificare ottenendo:178/33.