Maturità Scientifica 2017 – Questionario – Quesito 7 – Matematica

Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.

Traccia del Quesito 7 del Questionario Maturità Scientifica 2017

Determinare le coordinate dei centri delle sfere di raggio √6 tangenti al piano π di equazione x+ 2y−z+1= 0 nel suo punto P di coordinate (1; 0; 2).

Maturità Scientifica 2017 – Questionario – Quesito 7

Svolgimento:

Questo settimo quesito del questionario della maturità scientifica 2017 richiede di nuovo conoscenze base di geometria nello spazio. In particolare ci serviranno l’equazione del piano e della sfera, nonché l’applicazione delle condizioni di tangenza sfera piano.

Il piano π di equazione x+ 2y−z+1= 0 ha vettore normale n(1,2,-1). Il raggio delle due sfere tangenti, una per lato, è parallello a n e deve passare per P(1; 0; 2); anzi i raggi delle due sfere cercate è un segmento della retta passante per P e che ha direzione n.

Scriviamo quindi l’equazione di questa retta. In generale dato un punto P(P_x,P_y,P_z) e un vettore direzione n(n_x,n_y,n_z), la retta r è data da:

       /   x= P_x + n_xt
r: <      y=P_y + n_yt
      \    z=P_z + n_zt

con t ∈ R.  

Quindi con P(1; 0; 2) e n(1,2,-1):

      /    x= 1 + t
r: <      y= 2t
     \     z= 2 – t

con t ∈ R.  

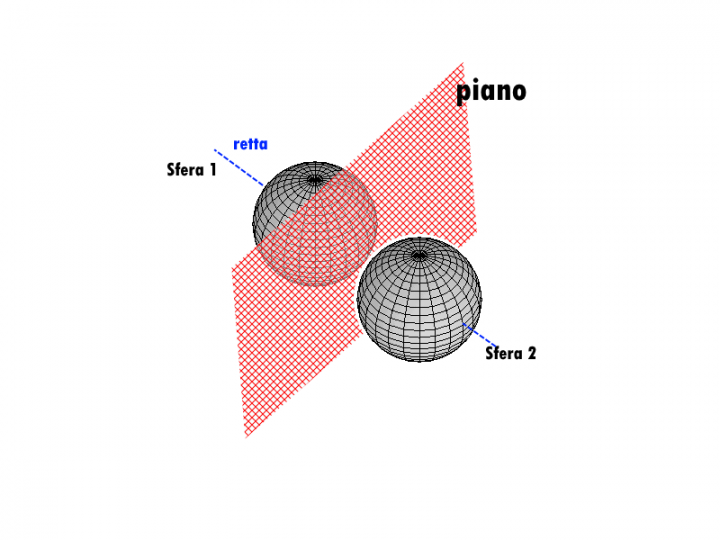
I raggi appartengono a questa retta. Notiamo che ovviamente anche i centri delle due sfere apparterranno a r. Il raggio sappiamo deve essere pari a √6. Quindi dobbiamo trovare un punto per lato, sulla retta r, tale che la sua distanza dal piano π sia appunto R=√6. La distanza Punto-Piano in generale è data da:

d(P,π)=|ax₀+by₀+cz₀+d|/√(a²+b²+c²)

dove: a,b,c,d sono i coefficienti dell’equazione del piano; mentre x₀,y₀,z₀ sono le coordinate del punto. 

Nel nostro caso, il punto è il centro della sfera e deve appartenere alla retta r, perciò sarà sempre nella forma:

       /    Cx= (1 + t)
C: <      Cy= (2t)
       \    Cz= (2 – t)

con t ∈ R.

Troviamo quindi C(Cx,Cy,Cz), il centro delle sfere e particolarizziamo t:

d(C,π)=|1•C_x+2•C_y+-1•C_z+1|/√(1²+2²+(-1)²)

d(C,π)=|1•(1+t)+2•(2t)-1•(2-t)+1|/√(1+4+1)

d(C,π)=|1+t+4t–2+t+1|/√6

d(C,π)=|6t|/√6

√6=|6t|/√6

eleviamo al quadrato e togliamo il valore assoluto:

6=36t²/6

6=6t²

t² = 1

quindi

t=-1 e t=+1 

e i centri saranno:

          /    C1x=  0
C1: <       C1y= -2
         \     C1z=  3

          /    C2x= 2
C2: <       C2y= 2
         \     C2z= 1

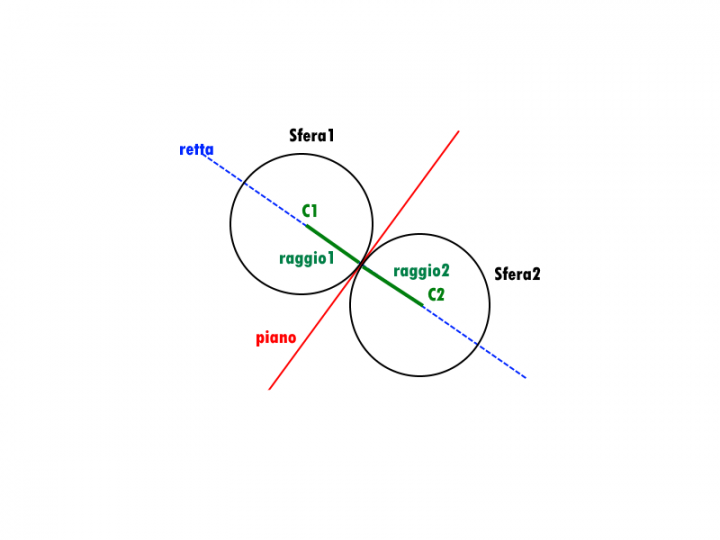
Sezione di piano e sfere

Link per approfondire la prova di maturità scientifica 2017, matematica.

• Vai al Questionario – Quesito 1 – 2017
• Vai al Questionario – Quesito 2 – 2017
• Vai al Questionario – Quesito 3 – 2017
• Vai al Questionario – Quesito 4 – 2017
• Vai al Questionario – Quesito 5 – 2017
• Vai al Questionario – Quesito 6 – 2017
• Vai al Questionario – Quesito 7 – 2017
• Vai al Questionario – Quesito 8 – 2017
• Vai al Questionario – Quesito 9 – 2017
• Vai al Questionario – Quesito 10 – 2017
• Vai al Problema 1 – Quesito 1 – 2017
• Vai al Problema 1 – Quesito 2 – 2017
• Vai al Problema 1 – Quesito 3  – 2017
• Vai al Problema 1 – Quesito 4  – 2017
• Vai al Problema 2 – Quesito 1 – 2017
• Vai al Problema 2 – Quesito 2 – 2017
• Vai al Problema 2 – Quesito 3 – 2017
• Vai al Problema 2 – Quesito 4 – 2017
• La geometria analitica nello spazio (ppt)

Random Post

PREVISIONE LOTTO n°87 di SABATO 20 LUGLIO 2019

PREVISIONE LOTTO n°87 di SABATO 20 LUGLIO 2019 Esito della previsione precedente: 2)NAZIONALE : 1 euro 10eLotto. (1) In parentesi tonda, eventuali risultati rilevanti (ambo, terno, ecc) su altre ruot... Vai al post...

Cammello, cammelli – Interpretazione dei sogni

Sognare un cammello, o una mandria di cammelli: significati, interpretazioni e numeri associati. Il cammello nel sogno è un simbolo di resistenza, e irrequietezza. Il cammello è un animale che, nono... Vai al post...

Ombrello, ombrelli – Interpretazione dei sogni

Sognare un ombrello, aperto, chiuso, rotto: significati, simbologia, interpretazioni e numeri della smorfia associati al sogno. L’ ombrello è una salvezza dalla pioggia o dal sole cocente, ma... Vai al post...

---

PUBBLICITÀ

---

Disclaimer: Questo blog NON è un prodotto editoriale ai sensi della legge n° 62 del 7 marzo 2001. Le immagini tratte da internet che possano violare i diritti di autore, previa comunicazione, attraverso la sezione -contatti-, verranno prontamente rimosse o sostituite.

Copyright: I contenuti presenti su ROMOLETTO BLOG dei quali è autore il proprietario del blog non possono essere copiati, riprodotti, redistribuiti perché appartenenti all autore stesso. Si vieta la copia e la riproduzione dei contenuti in qualsiasi modo o forma. Si vieta altresì la pubblicazione e la redistribuzione dei contenuti non autorizzata espressamente dell autore.

---

Copyright © 2011 / 2020 - ROMOLETTO BLOG - All Right Reserved

---

Informazioni su Romoletto Blog

Ingegnere Civile, Blogger, Programmatore VB.NET, Lezioni private per scuole medie inferiori e superiori. Per contattarmi scorri la home fino in fondo e vai al form -Contatti-

Visualizza tutti gli articoli di Romoletto Blog →