Maturità Scientifica 2017 – Questionario – Quesito 2

by Romoletto Blog · 11 Luglio 2017

Maturità Scientifica 2017 – Questionario – Quesito 2 – Matematica

Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.

[el58862bfc101c9]

Traccia del Quesito 2 del Questionario Maturità Scientifica 2017

Una torta di forma cilindrica è collocata sotto una cupola di plastica di forma semisferica. Dimostrare che la torta occupa meno dei 3/5 del volume della semisfera.

Maturità Scientifica 2017 – Questionario – Quesito 2

Romoletto Blog ti consiglia...

4x50 capsule Borbone Don Carlo DEGUSTAZIONE 50 NERA, 50 BLU, 50 RED, 50 ORO compatibili a modo mio

Attenzione: verifica i tempi di consegna. Con joebreak2016 ti arriva prima.. ...
Nota: prodotto fornito da Amazon

Svolgimento:

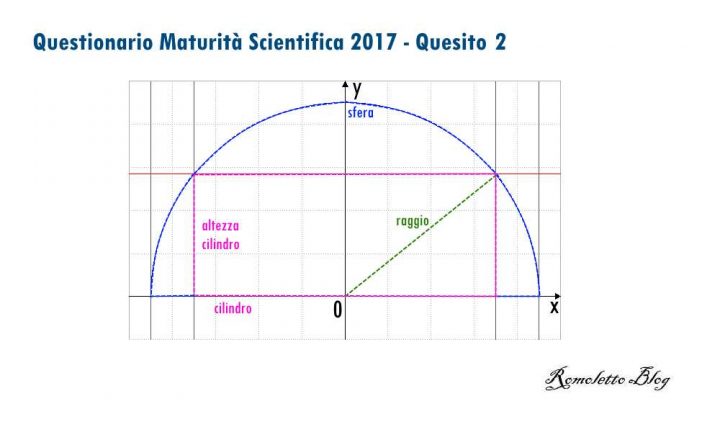
Questo secondo quesito del questionario della prova di matematica della maturità scientifica 2017 richiede, in pratica, di dimostrare che qualsiasi cilindro metto sotto la semisfera, questo sarà, in volume, sempre minore dei 3/5 di quello della cupola. Partiamo con un ragionamento semplice: i cilindri possono variare tra quelli di base con cerchio con raggio pari a quello della semisfera R (il cilindro coincide con il cerchio massimo della sfera) e quelli con raggio zero ma altezza massima pari appunto al raggio R, ma con area di base nulla.

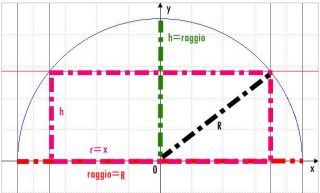
Cilindri nella semisfera - Questionario - Quesito 2

Cilindri possibili nella semisfera

Tra tutti questi dobbiamo trovare quello con volume maggiore e vedere se risulta essere inferiore ai 3/5 del volume della semisfera. Si tratta perciò di un problema di ricerca di massimi.

Vediamo anzitutto il volume della semisfera:

V_semisfera=½V_sfera= ½[4(πR³)]/3=[2(πR³)]/3

Il volume del cilindro in generale è:

V_cilindro= A_base x h_altezza = πhr²

Esprimo il raggio in funzione di x, ottenendo così:

V_cilindro= πhx²

A sua volta anche l’altezza è funzione x (e di R ) in quanto, per il teorema di Pitagora:

h=√ (R² – x²)

Sostituendo:

V_cilindro= πx2√(R²-x²)

Per trovare il massimo di questa espressione dobbiamo derivare:

V’_cilindro= [f(x)g'(x) + f'(x)g(x)]
(Derivata del prodotto di funzioni), dove:
f(x)=πx²
f'(x)=2πx
g(x)=√(R²-x²)
g'(x)=½(-2x)/(√(R²-x²))= -x/√(R²-x²)
quindi:
V’_cilindro= [πx² (-x)/√(R²-x²) + 2πx √(R²-x²)] =
= π( -x³+ 2R²x-2x³)/√(R²-x²)=
=(2πR²x – 3πx³)/√(R²-x²)

Il massimi (o minimi) sono in corrispondenza dei valori che annullano la derivata prima; poichè è un’equazione fratta, posto che x≠R², studio quando si annulla il numeratore:

(2πR²x – 3πx³) =0
πx(2R²-3x²)=0

Le soluzioni sono:
x=0 (che si scarta, il cilindro sarebbe un segmento) oppure:

x²=(2/3)R²

da cui:
x=±R√(2/3)

Dobbiamo controllare se effettivamente si tratta di massimi; per cui studiamo anche il segno di numeratore e denominatore:

N(x)≥0 ⇔ -R√(2/3) ≤ x ≤ +R√(2/3) (valori interni, equazione di secondo grado, coefficiente ‘a’ =1 >0, segno disequazione ‘<‘)

D(x)>0 ⇔ -R ≤ x ≤ +R (valori interni, equazione di secondo grado, coefficiente ‘a’ =1 >0, segno disequazione ‘<‘)

Dallo studio del segno e tenendo conto della simmetria, si può studiare il tutto nel primo quadrante (ottante in realtà):

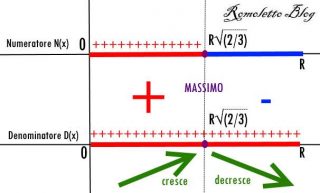
Segno della derivata

Come si vede dal grafico, la derivata prima cresce e poi decresce, perciò x_max=R√(2/3) e simmetricamente lo è anche -R√(2/3). Ora bisogna controllare se il volume di questo cilindro “massimo” è inferiore ai 3/5 di V_semisfera. Il valore di x è il valore del raggio che mi da area massima nel primo quadrante e di conseguenza volume massimo. Andiamo a calcolare Vcilindro:

V_cilindro= A_base x h_altezza

r=R√(2/3)
h=√ [(R² – (R√(2/3))²] = R² – (2/3) R² = (1/3)R²

V_cilindro= (1/3)√(2/3) πR³ = √(2/27) (πR³)

passiamo alla semisfera:

V_3/5semisfera= (3/5)[2(πR³)]/3 =(2/5)(πR³)

Quindi:

√(2/27) (πR³) < (2/5)(πR³) (?)
√(2/27) < (2/5) (?)
(5/2)√(2/27) < 1 (?)
√(2*25/4*27) <1 (?)
√(50/108) <1
0,68<1

il rapporto è inferiore a 1 per cui anche la radice quadrata di un numero inferiore a 1 è inferiore a 1 e quindi il massimo cilindro inseribile dentro la cupola è più piccolo dei 3/5 del suo volume.