Maturità Scientifica 2017 – Problema 2 – Quesito 2
Maturità Scientifica 2017 – Problema 2 – Quesito 2 – Matematica
Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.
[el58862bfc101c9]
Traccia del Problema 2 della Maturità Scientifica 2017 – Quesito 2
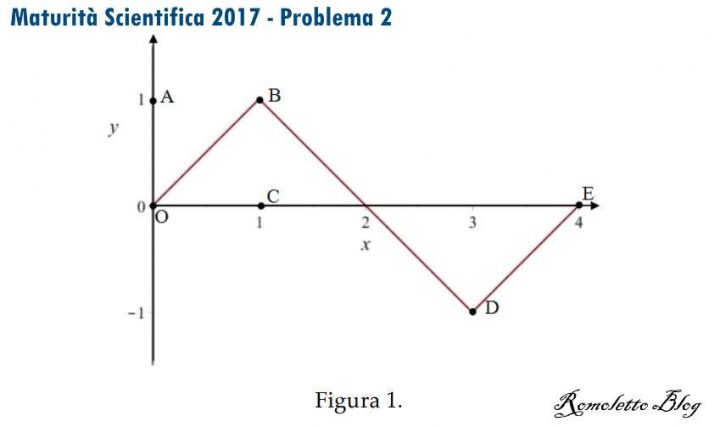
Consideriamo la funzione f : R → R , periodica di periodo T=4 il cui grafico, nell’intervallo [0;4], è il seguente:
Figura 1 Problema 2 Quesito 2 Maturità Scientifica 2017
Come si evince dalla Figura 1, i tratti OB, BD, DE del grafico sono segmenti i cui estremi hanno coordinate:
O(0; 0), B(1; 1), D(3; −1), E(4; 0).
Quesito 2: Considera la funzione: s(x) = sin(bx), con b costante reale positiva. determina b in modo che s(x) abbia lo stesso periodo di f(x).
Dimostra che la porzione quadrata di piano OABC in Figura 1 viene suddivisa dai grafici di f(x) e s(x) in 3 parti distinte e determina le probabilità che un punto preso a caso all’interno del quadrato OABC ricada in ciascuna delle 3 parti individuate.
Svolgimento:
Questo quesito richiede di determinare una costante reale e positiva b, tale che il sen(bx) abbia periodo T = 4. La funzione y = sen(x), con b*=1 quindi, ha periodo, come è noto, T*=2π. Inoltre se una funzione y=f(x) è periodica di periodo T, allora la funzione y=(kx), con k reale diverso da zero, è periodica di periodo T/|k|. Nel nostro caso il periodo della funzione g(x) = sen(bx) deve essere T=T*/b, dove T* è il periodo della funzione sen(x) e T è quello dato. Quindi sostituendo:
4 = 2π/b
b=2π/4=π/2.
b=π/2
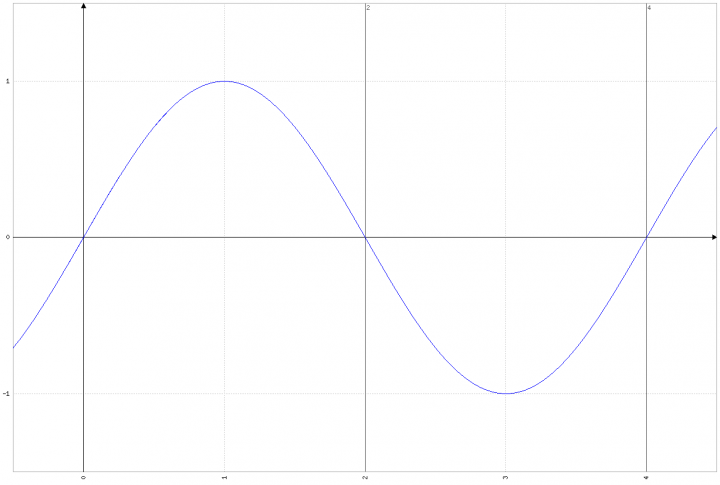
Per controllo vediamo gli zeri:
x=0 → sen (x· π/2) = sen ( 0) = 0 (OK)
x=2 → sen (x· π/2) = sen ( π) = 0 (OK)
x=4 → sen (x· π/2) = sen (2π) = 0 (OK)
Le tre parti in cui viene suddiviso il quadrato OABC sono illustrate di seguito:
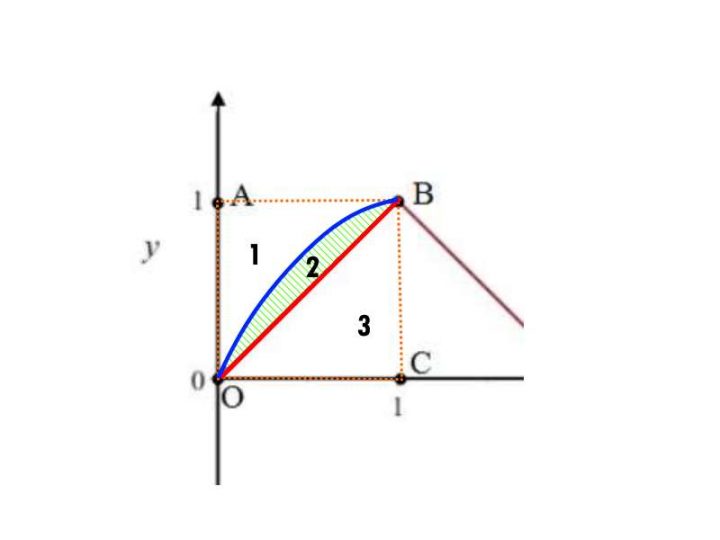
Le tre parti in cui è suddiviso il quadrato OABC
Il quesito chiede di “dimostrare” che si formano 3 parti distinte: graficamente lo si vede subito; analiticamente si può dire che OB è la diagonale e che quindi già suddivide in 2 parti il quadrato, bisogna solo vedere se g(x) interseca la retta OB in altri punti che non siano gli estremi O e B (cioè considerando x∈(0,1)). E cosi è, anche mettendo a sistema:
y = x e y = sen(½πx) si ha che: x = sen(½πx) quindi
arcsen(x)= ½ π x → arcsen(x)/x = ½ π
Ricordando che l’arcoseno tra (0,1) varia tra (0, π/2) e che x varia tra (0,1) e che il loro rapporto è sempre maggiore di 1 (è uguale a ½ π infatti), significa appunto che il numeratore è sempre maggiore del denominatore. Quindi in questo caso sta sempre sopra e non si incontrano mai.
Per quanto riguarda l’ultima parte, il quesito vuole semplicemente che si calcolino le aree A1, A2, e A3 la cui somma totale deve dare l’area del quadrato Aq. Con un semplice proporzione si ricaverà appunto la probabilità richiesta.
Aq = l2 = 1
A3= Aq/2 = ½
A2 = Asinusoide – A3
ricordando che :
∫sen[f(x)] · f ‘(x) dx = – cos[f(x)] + c
andiamo a calcolare l’integrale seguente:
1 1
Asinusoide= ∫ sin(½ π x) dx = -[2 cos(½ π x)/π] = 2/π
0 0
A2=2/π -½ = (4-π)/(2π) ≅ 0,637-0,5=0,137
A1= Aq – Asinusoide = 1- 2/π ≅ 1-0,637=0,363
Poichè la probabilità totale è sempre 1, e fortunatamente coincide con l’area del quadrato, non occorrono pertanto ulteriori calcoli; se cosi non fosse stato si sarebbero dovute rapportare le varie aree A1, A2, A3 alla Aq e fare delle proporzioni. Quindi:
Ptot(Aq)=1,000 → 100,0%
P1(A1)=0,363 → 36,3%
P2(A2)=0,137 → 13,7%
P3(A3)=0,500 → 50,0%
Link per approfondire la prova di maturità scientifica 2017, matematica.
- Vai al Questionario – Quesito 1 – 2017
- Vai al Questionario – Quesito 2 – 2017
- Vai al Questionario – Quesito 3 – 2017
- Vai al Questionario – Quesito 4 – 2017
- Vai al Questionario – Quesito 5 – 2017
- Vai al Questionario – Quesito 6 – 2017
- Vai al Questionario – Quesito 7 – 2017
- Vai al Questionario – Quesito 8 – 2017
- Vai al Questionario – Quesito 9 – 2017
- Vai al Questionario – Quesito 10 – 2017
- Vai al Problema 1 – Quesito 1 – 2017
- Vai al Problema 1 – Quesito 2 – 2017
- Vai al Problema 1 – Quesito 3 – 2017
- Vai al Problema 1 – Quesito 4 – 2017
- Vai al Problema 2 – Quesito 1 – 2017
- Vai al Problema 2 – Quesito 2 – 2017
- Vai al Problema 2 – Quesito 3 – 2017
- Vai al Problema 2 – Quesito 4 – 2017
- Funzioni periodiche (wikipedia)
- Nozioni base di Probabilità