Maturità Scientifica 2017 – Problema 1 – Quesito 1
Maturità Scientifica 2017 – Problema 1 – Quesito 1 – Matematica
Una serie di problemi di matematica delle Prove di Maturità del Liceo Scientifico risolti durante le ripetizioni date a studenti. Maturità Scientifica 2017 è la raccolta delle tracce 2017 e dello svolgimento dei relativi problemi di difficoltà alta, sia per ragionamenti e competenze necessarie che per via del tempo di svolgimento. A questo link la traccia completa in pdf.
[el58862bfc101c9]
Traccia del Problema 1 della Maturità Scientifica 2017 – Quesito 1
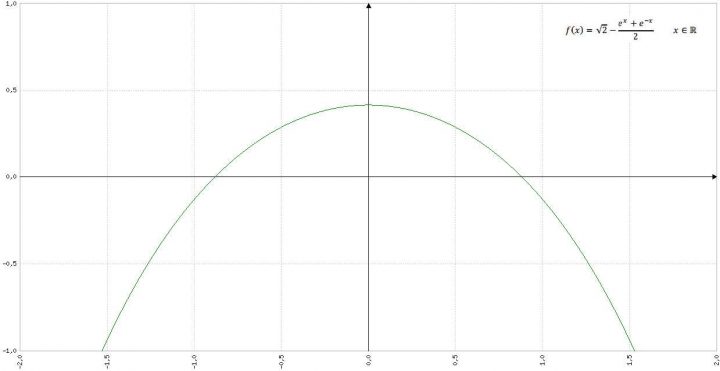
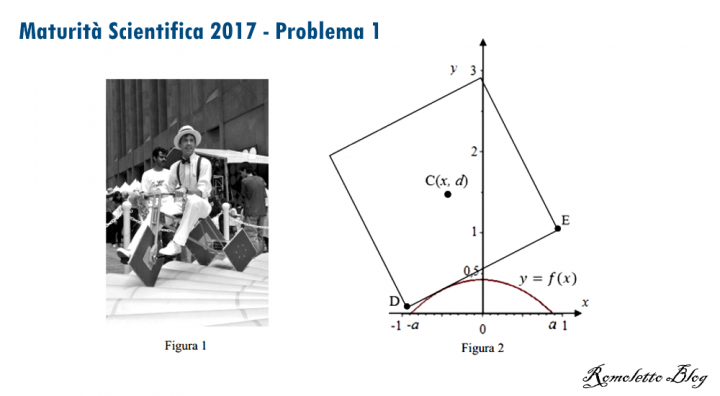
Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New York, al MoMath-Museum of Mathematics si può fare, in uno dei padiglioni dedicati al divertimento matematico (figura 1). È però necessario che il profilo della pedana su cui il lato della ruota può scorrere soddisfi alcuni requisiti. In figura 2 è riportata una rappresentazione della situazione nel piano cartesiano Oxy: il quadrato di lato DE= 2 (in opportune unità di misura) e di centro C rappresenta la ruota della bicicletta, il grafico della funzione f(x) rappresenta il profilo della pedana.
Quesito 1: Sulla base delle informazioni ricavabili dal grafico in figura 2, mostra, con le opportune argomentazioni, che la funzione:
Figura 2
rappresenta adeguatamente il profilo della pedana per x ∈ [−a ; a]; determina inoltre il valore degli estremi a e – a dell’intervallo.
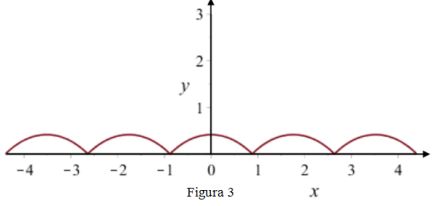
Figura 3
Per visualizzare il profilo completo della pedana sulla quale la bicicletta potrà muoversi, si affiancano varie copie del grafico della funzione f(x) relativo all’intervallo [−a ; a], come mostrato in figura 3.
Maturità Scientifica 2017 – Problema 1
Svolgimento:
Questo primo quesito di maturità scientifica 2017, che potrebbe di primo acchito un po’ spiazzare, in quanto si potrebbe non capire cosa voglia si faccia, chiede in sostanza di verificare che la ruota quadrata, per muoversi, descriva proprio la curva identificata dalla funzione y=f(x). O meglio: ci chiede di mostrare che quella equazione matematica quantomeno somigli al grafico in rosso e che ne abbia le caratteristiche peculiari. La prima cosa che notiamo è che, quel grafico, nell’intervallo [-a,a] è simmetrico rispetto all’asse y, non ha discontinuità, è prima crescente e poi decrescente, (in x=-a e x=a , come si evince dalla figura 3, si hanno un punti angolosi), con un massimo chiaramente individuabile in x=0, che deve valere un po’ meno di 0,5. La funzione inoltre deve essere convessa, perchè appunto il grafico che vediamo è convesso. Infine interseca l’asse x proprio in x = -a e x = a e dalla figura a deve vale un po’ meno di |1|. Quindi passiamo a verificare se quanto vediamo con gli occhi è ben rappresentato dalla y=f(x) in questione:
- Simmetria rispetto all’asse y: f(x) = f(-x)
- Continuità (campo di esistenza): {∀x∈R}
- Crescenza, decrescenza: f ‘(x) ≥ 0
- Massimi, minimi: f ‘(x)=0
- Concavità, convessità: f ”(x) ≥ 0
- Intersezione con l’asse delle ascisse.
1) Simmetria rispetto all’asse y: f(x) = f(-x)
(√2 – (ex + e-x)/2) ?=? (√2 – (e-x + ex)/2)
√2 – (ex + e-x)/2 = √2 – (e-x + ex)/2ex + e-x = e-x + ex
0=0
La funzione è simmetrica rispetto all’asse y.
2) Continuità (campo di esistenza): {∀x∈R}
La funzione è somma e prodotto di costanti e di funzioni esponenziali che sono definite per tutti i valori reali e sono sempre positive in particolare è continua anche in [-a,a] anche perchè qui la funzione esponenziale e-x = 1/ex non assume mai valore zero.
3) Crescenza, decrescenza: f ‘(x) ≥ 0
Ricordando che la per y=ef(x) y′=ef(x)⋅f′(x) :
f'(x)= – (ex-e-x)/2 = (e-x – ex)/2
e-x – ex ≥ 0
ln(e-x ) ≥ ln(ex)
-x ≥ x
2x ≤ 0
x≤ 0
Quindi per x ≤ 0 la funzione è crescente (e dopo è decrescente). Questo già è sufficiente a dire che in x=0 è presente un massimo e che anche convessa. Per completezza calcoliamo il max e studiamo la derivata seconda.
4) Massimi, minimi: f ‘(x)=0
f'(x) = (e-x – ex)/2 = 0
e-x – ex = 0
x=0 ⇒ f(x=0) = 1,41 – (1+1/1)/2 ≅ 0,41
5) Concavità, convessità: f ”(x) ≥ 0
f ”(x) = (-e-x – ex)/2 ≥ 0
-(e-x + ex) ≥ 0
la funzione esponenziale è sempre positiva, la somma di due quantità positive è ancora positiva, moltiplicata per meno è sempre una quantità negativa.
Poiché la derivata seconda è sempre negativa vuol dire che la funzione in questione è sempre convessa.
6) Intersezione con l’asse delle ascisse
√2 – (ex – e-x)/2 = 0
2√2 – ex + e-x = 0
2√2 – ex + 1/ex =0
2√2 ex – e2x =0
ponendo ex = t , e2x = t2
t2 – 2√2 t +1=0
da cui:
Δ = 8-4=4 ⇒ √Δ =2
t1,2 = (- 2√2 ± 2 )/2
t1 = √2 – 1 ; t2 = √2 + 1
ex12= √2 – 1 ; ex22= √2 + 1
x1= ln(√2 – 1) ; x2= ln(√2 + 1)
quindi:
-a = ln(√2 – 1)≅-0,88 ; a = ln(√2 + 1)≅0,88
Abbiamo confermato che a è una quantità poco inferiore a 1 come visibile dal grafico e ne abbiamo calcolato il valore pari a circa 0,88 come richiesto.
Osservazioni varie:
Tra le cose che possiamo notare è che questa bicicletta, muovendosi, mantiene il centro C della ruota (quadrata) rimane sempre alla stessa distanza dall’asse x. Se cosi non fosse la bicicletta sobbalzerebbe o comunque avrebbe un andamento altalenante.
Quindi un punto fermo è che:
d(C,r: y=0)=d=costante.
Notiamo che nella posizione iniziale (e finale), ovvero quando C e D (o C ed E) sono allineati verticalmente, la distanza CD corrisponde alla semidiagonale del quadrato:
Ricordando che il rapporto tra lato è diagonale di un quadrato è d=l· √2
CD= (2*√2)/2 = √2
Quindi la distanza costante di cui sopra deve valere:
d(C,r: y=0)= √2
Nella posizione intermedia, ovvero quando il centro è allineato con l’origine la distanza CO corrisponde al semilato del quadrato a cui si deve aggiungere una certa quantità PO. Ovviamente, in una posizione intermedia:
CO = CP+PO = d(C,r: y=0) = √2
quindi: il semilato è (l/2)=(2/2)=1; La posizione yp =√2 -1 = 0,41 che conferma quanto già calcolato.
Una ulteriore osservazione che potrebbe essere utile è che il lato del quadrato contenuto in una retta, chiamiamola q, nel punto P deve essere sempre tangente alla funzione. Ciò significa che il sistema deve avere determinante sempre diverso da zero. Altra osservazione è la lunghezza del lato del quadrato deve coincidere con la lunghezza della curva.
Infine il grafico della catenaria in questione:
Link per approfondire la prova di maturità scientifica 2017, matematica.
- Vai al Questionario – Quesito 1 – 2017
- Vai al Questionario – Quesito 2 – 2017
- Vai al Questionario – Quesito 3 – 2017
- Vai al Questionario – Quesito 4 – 2017
- Vai al Questionario – Quesito 5 – 2017
- Vai al Questionario – Quesito 6 – 2017
- Vai al Questionario – Quesito 7 – 2017
- Vai al Questionario – Quesito 8 – 2017
- Vai al Questionario – Quesito 9 – 2017
- Vai al Questionario – Quesito 10 – 2017
- Vai al Problema 1 – Quesito 1 – 2017
- Vai al Problema 1 – Quesito 2 – 2017
- Vai al Problema 1 – Quesito 3 – 2017
- Vai al Problema 1 – Quesito 4 – 2017
- Vai al Problema 2 – Quesito 1 – 2017
- Vai al Problema 2 – Quesito 2 – 2017
- Vai al Problema 2 – Quesito 3 – 2017
- Vai al Problema 2 – Quesito 4 – 2017
- Pedalare con una bicicletta con le ruote quadrate
- La catenaria (wikipedia)
- Testo della traccia in pdf dal sito Zanicchelli
- Svolgimento della prova su TomwHw.it
- Quaderni di laboratorio 2009 – Una non parabola: la catenaria con qualche cenno al calcolo della sua equazione. Franco Ghione