Parabola – Geometria Analitica
Matematica – La parabola.
Definizioni:
La parabola è il luogo geometrico dei punti equidistanti da una retta (chiamata direttrice) e da un punto fisso detto fuoco. Fa parte della famiglia delle coniche. La retta passante per il fuoco e perpendicolare alla direttrice si chiama asse della parabola. L’ asse della parabola è un asse di simmetria e la interseca nel vertice.
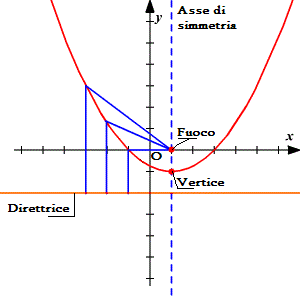
Esempio di parabola
La condizione quindi da rispettare per ottenere questa conica è che PF=FD. Per il punto P passano poi due rette particolari: la retta tangente la curva e la normale alla tangente, tra loro ortogonali ovviamente.
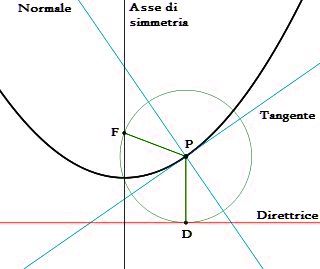
Condizione FP=PD
Una parabola con asse di simmetria parallelo all’asse y è rappresentata da un’equazione del tipo:
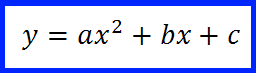
Equazione tipo
Se è a>0, la concavità della parabola è rivolta verso l ‘alto; se a <0 la ,verso il basso.
Il vertice ha coordinate:
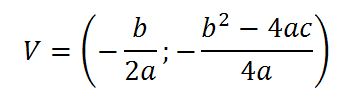
Il fuoco ha coordinate:
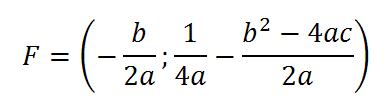
L’equazione dell’ asse di simmetria sarà quindi:
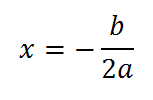
e l’equazione della direttrice:
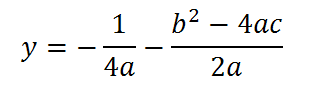
Esempio:
Rappresentare graficamente la parabola di equazione:
![]()
Quindi: a=2; b=-1;c=3.
Il vertice avrà coordinate:
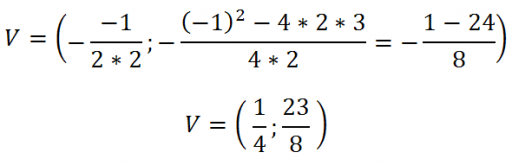
Il fuoco avrà coordinate:
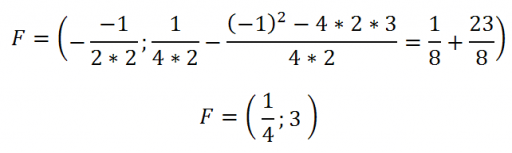
L’asse di simmetria e la direttrice hanno rispettivamente equazione:
![]()
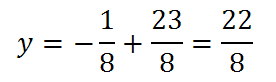
A questo punto è opportuno trovare le intersezioni con gli assi cartesiani, facendo sistema appunto una volta tra x=0 (asse y) e l’equazione e una volta tra y=0 (asse x) e sempre l’equazione della nostra conica. Avremo quindi rispettivamente sostituendo:
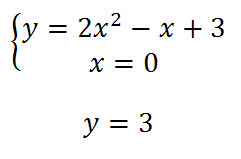
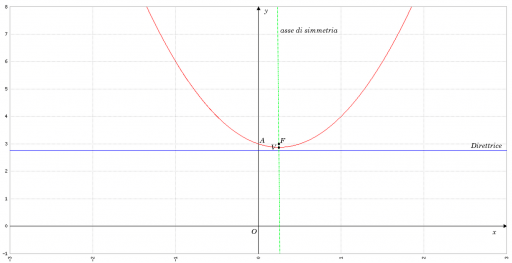
Ottengo un punto di intersezione con l’asse y in A(0;3).
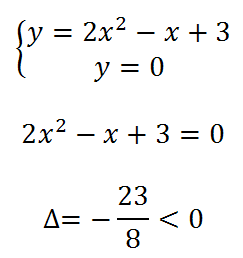
Non ottengo alcuna intersezione con l’asse x, in quanto il discriminante dell’equazione di secondo grado è negativo.
Graficamente: