Campo di esistenza di funzioni matematiche – I
Il campo di esistenza delle funzioni matematiche. Definizioni e applicazione alle funzioni più comuni. Prima parte
Il campo di esistenza di una funzione può essere semplicemente descritto come “l’insieme dei valori che posso dare alla variabile indipendente senza ottenere errori di indeterminatezza o impossibilità”.
Definizioni:
-
Dati due insiemi A e B entrambi appartenenti a R, si definisce funzione una legge che fa corrispondere a un elemento di A uno e un solo elemento di B. A è detto dominio della funzione, B è detto codominio.
-
Si definisce campo di esistenza di una funzione l’insieme dei valori che si possono attribuire alla variabile x per ottenere il valore della y.
- La differenza tra dominio e campo di esistenza è sottile e generalmente senza errore si usano i due termini come sinonimi: il campo di esistenza è l’insieme dei valori della x per i quali f(x) ha senso. Il dominio invece è l’insieme in cui è definita la funzione. Esempio: La funzione f(x) = √x è ha senso per tutto RO+ (campo di esistenza), tuttavia si potrebbe specificare un dominio costituito dai soli numeri pari positivi.
Esempio di funzione matematica.
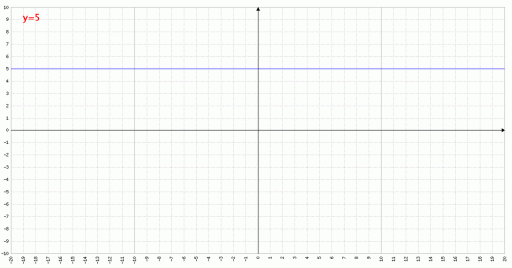
Campo di esistenza della Funzione Costante:
\(y=k ; \, k\epsilon \mathbb{R}\)
E’ rappresentata graficamente da una retta parallela all’asse delle ascisse posta a distanza k. Anche se la x non compare da nessuna parte, è “grosso modo” come avere la funzione:
\(y={\frac{kx}{x}}{} ; \, k\epsilon \mathbb{R}\)
Il campo di esistenza della funzione è tutto R, infatti per qualsiasi valore di x, l’immagine sarà sempre k.
\(D: \left \{ x/x \epsilon \mathbb{R} \right \} \)
Esempio:
Funzione costante
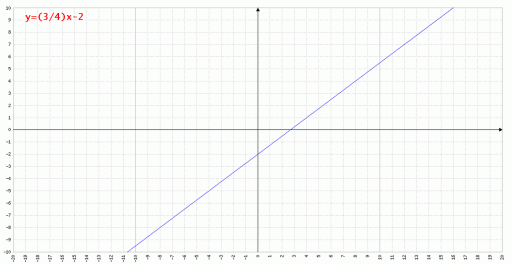
Funzione Lineare:
\(y=ax+b;\: a,b \epsilon \mathbb{R} \)
Graficamente questa funzione è una retta inclinata con inclinazione (coefficiente angolare) pari ad a; b rappresenta il punto di intersezione con l’asse delle ordinate.
Il campo di esistenza della funzione è tutto R, infatti per qualsiasi valore di x è possibile ricavare l’immagine.
\(D: \left \{ x/x \epsilon \mathbb{R} \right \} \)
Esempio:
Funzione lineare
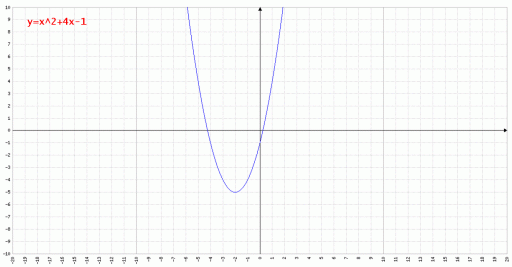
Funzione Quadratica:
\(y=ax^2+bx+c;\: a,b,c \: \epsilon \: \mathbb{R} \; a\neq 0\)
Graficamente questa funzione è una parabola ad asse parallelo all’asse delle ordinate, con vertice :
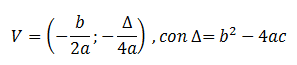
La concavità è rivolta verso l’alto se a>0 viceversa verso il basso se a<0. Il campo di esistenza della funzione è tutto R, infatti per qualsiasi valore di x è possibile ricavare l’immagine.
\(D: \left \{ x/x \epsilon \mathbb{R} \right \} \)
Esempio:
Funzione quadratica
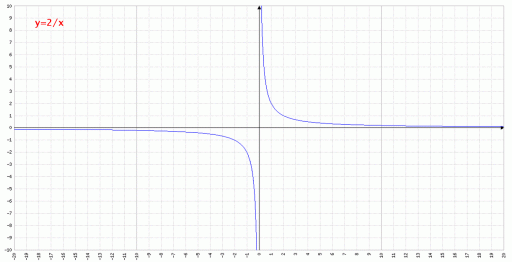
Funzione di proporzionalità inversa:
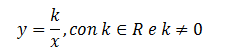
Graficamente è una iperbole equilatera con asintoti i semiassi del primo e terzo quadrante se k>0 viceversa a quelli del secondo e quarto se k<0. Il campo di esistenza della funzione è tutto R tranne il valore di x che annulla il denominatore, infatti per quel valore la funzione assume valore infinito.
Esempio:
Funzione di proporzionalità inversa
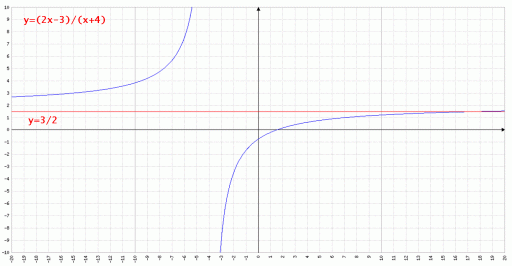
Funzione omografica:
Graficamente questa funzione rappresenta una iperbole equilatera con asintoti :
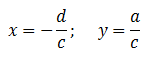
Il campo di esistenza della funzione è tutto R tranne il valore di x che annulla il denominatore , infatti per quel valore la funzione assume valore infinito; deve essere perciò:
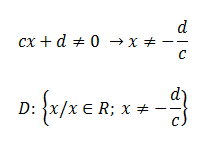
Esempio:
Funzione omografica
