Asintoti obliqui – Matematica
Gli asintoti obliqui di una funzione matematica
In generale gli asintoti sono delle rette alle quali i punti della funzione si avvicinano indefinitamente all’infinito. Gli asintoti possono essere orizzontali, verticali od obliqui. In particolare gli asintoti obliqui sono delle rette inclinate rispetto all’asse delle ascisse. In questo articolo si studierà l’asintoto obliquo e come fare a determinarlo. In matematica, un altro modo di di parlare di asintoti è dire che esso è una retta tale che la distanza tra essa e la funzione y = f (x) tende a 0.
Asintoti obliqui
Se non esiste l’asintoto orizzontale (ovvero se il limiti orizzontali vengono ±∞) occorre controllare se esista l’asintoto obliquo; per determinarlo occorre effettuare questi due limiti:
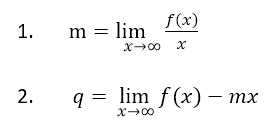
Condizioni Asintoto Obliquo
Per ammettere asintoto obliquo deve essere m≠0 (altrimenti sarebbe un asintoto orizzontale) e q non deve tendere a infinito. Questi due valori, m e q entrano sono i parametri della retta di equazione y=mx+q.
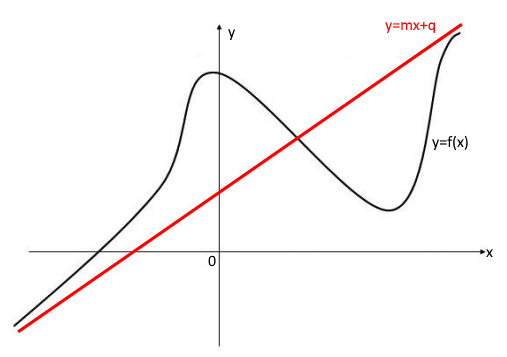
Asintoti obliqui – Matematica
La retta y = mx + q , se si studia il limite per x →+∞ , si dice Asintoto Obliquo Destro (A.Ob.D.). Viceversa, se si studia il limite per x →-∞ si parla di Asintoto Obliquo Sinistro (A.Ob.S.).
Note:
- Una funzione può ammettere al massimo due tra orizzontali e obliqui, se uno è orizzontale e l ‘altro è obliquo, devono stare in parti opposte (+∞ e -∞ e viceversa).
- Se il campo di esistenza è un intervallo limitato, non è necessario cercare nè asintoti orizzontali nè obliqui.
- Se la funzione è razionale intera non ci sono asintoti di nessun tipo.
- Se non esiste l’asintoto orizzontale non è detto che esista quello obliquo.
- Se è gia presente un asintoto orizzontale destro (sinistro) allora sicuramente non ha senso indagare sull’esistenza dell’asintoto obliquo di cui quello orizzontale è un caso particolare.